Physics presentation: ideal fluid flow

When this pump or vacuum system is started, air begins to flow through this hose, which has a slight crimp, and as a result this hose begins to totally collapse. Now don't you say it's because of suction, because as you know, physics don't suck. (It blows.) (Video link: "hose collapse.")

In a previous presentation we investigated the behavior of static fluids, now we'll consider dynamic fluids--more specifically, ideal fluid flow. First we'll define what we mean by "ideal" fluids, then we'll see how two conservation laws are applied simultaneously to flowing ideal fluids.

Ideal fluids fall under a restrictive class of fluids--let's take a look at the characteristics that set ideal fluids apart from, say, real fluids.

Ideal fluids are incompressible, which water is to some extent. Note that while air is not incompressible, there are situations where we can make the crude approximation that it is.

An ideal fluid should undergo laminar flow, where the adjacent particles flow smoothly past each other, as opposed to turbulent flow, where particles swirl around in a chaotic manner. Like many fluids water can undergo both laminar and turbulent flow, so we'll restrict our attention to certain conditions where water undergoes laminar flow.

Lastly, an ideal fluid should be non-viscous, that is, flow without appreciable frictional losses, as opposed to a viscous fluid that, well, looks and is literally, "gooey." (Video link: "Viscosity.")

Streamlines are a way to visualize ideal fluid flow. Here air is undergoing incompressible, laminar, non-viscous flow over the front end of a car in this wind tunnel, where the streamlines are smoothly conforming to the contours of the car and to adjacent streamlines. Note the rear of the car, where the streamlines are turbulent, and indicate the presence of non-ideal fluid flow. (Video link: "Mercedes-Benz SLS AMG Developement and Testing Wind tunnel.")

The first conservation law for ideal fluid flow follows from its incompressible nature.

Even if a pipe changes radius, the incompressibility of an ideal fluid means that the same volume flowing in one end must equal to the same volume coming out the other end in the same amount of time. "Stuff in, stuff out."

This conservation of volume flow rate can be reinterpreted in terms of cross-sectional areas and fluid speeds in the continuity equation. A large-area section of pipe will have a slower fluid speed than a small-area section of the same pipe, which will have a faster fluid speed. Note that the product of cross-sectional area and fluid speed at any section of a pipe results in the volume flow rate.

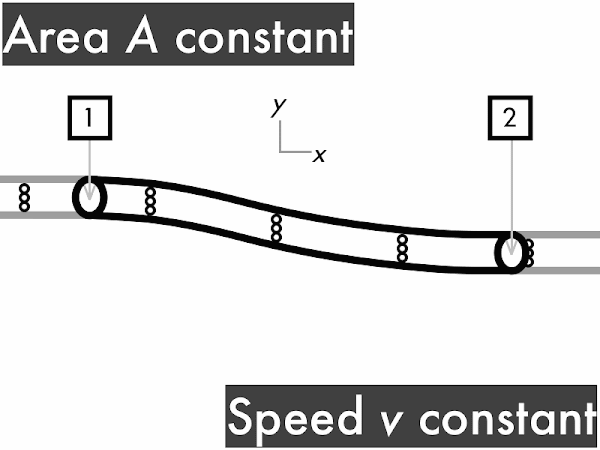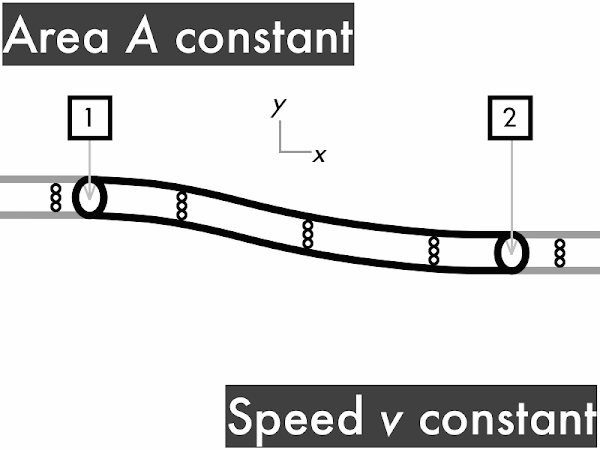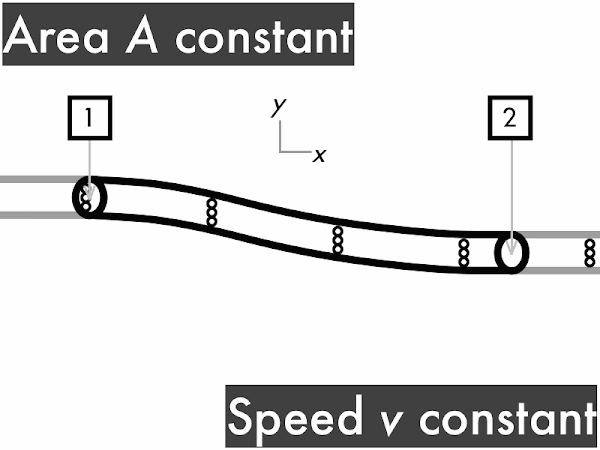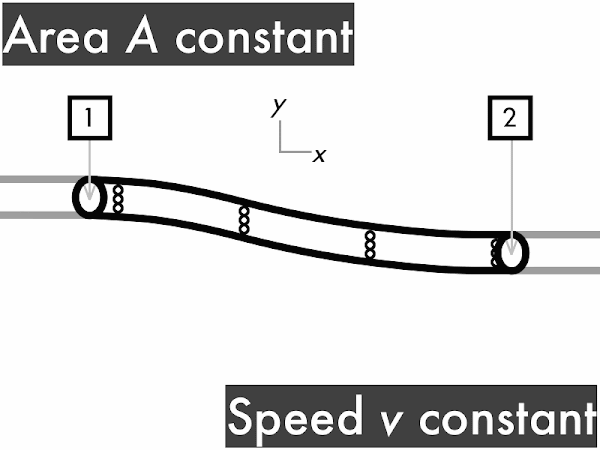
For a pipe with a constant cross-sectional area, the volume flow rate ∆V/∆t through the pipe is constant. To convince yourself of this you'll need a friend to watch this animation with you. Every time you see fluid particles entering the pipe, say "in." "In. In. In..." Keep doing that. Convince your friend to say "out" every time fluid particles are leaving the pipe. "Out. Out. Out..." If the two of you do this correctly, each time you say "in," your friend immediately follows-up by saying "out." This means that rate of fluid volume going in (represented here by three dots) must continuously be equal to the rate of fluid volume going out. "Stuff in, stuff out," right?

Then from the continuity equation:

A₁·v₁ = A₂·v₂,

since the cross-sectional areas of where the fluid goes in and where it goes out are the same (A₁ = A₂), then v₁ = v₂, so the speed of the fluid flowing through this pipe must be constant as well.

For a pipe with increasing cross-sectional area, the volume flow rate ∆V/∆t through the pipe is also constant. Let's do the same "in and out" exercise as above. Every time you see fluid particles entering the narrow end of the pipe, say "in," while your friend says "out" every time fluid particles are leaving the wider end of the pipe. "In. Out. In. Out. In. Out..." As before, since each time you say "in," your friend immediately follows-up by saying "out," so the rate of fluid volume going in the narrow end (represented here by three dots) must continuously be equal to the rate of fluid volume going out the wider end. "Stuff in, stuff out," right?

Then from the continuity equation:

A₁·v₁ = A₂·v₂,

since the cross-sectional area of where the fluid goes in is smaller than the cross-sectional area of where it goes out (A₁ < A₂), then v₁ > v₂, so the speed of the fluid flowing through this pipe slows down.

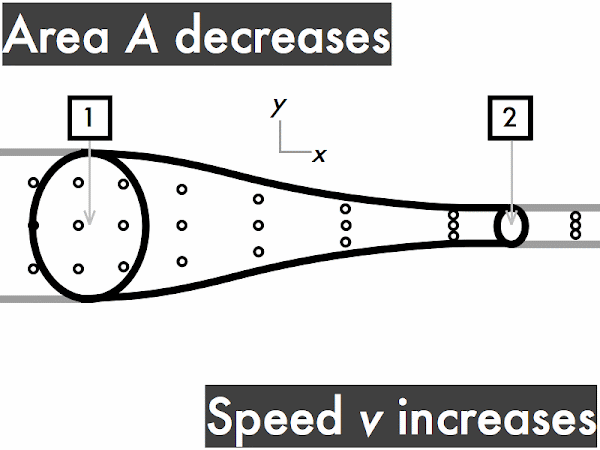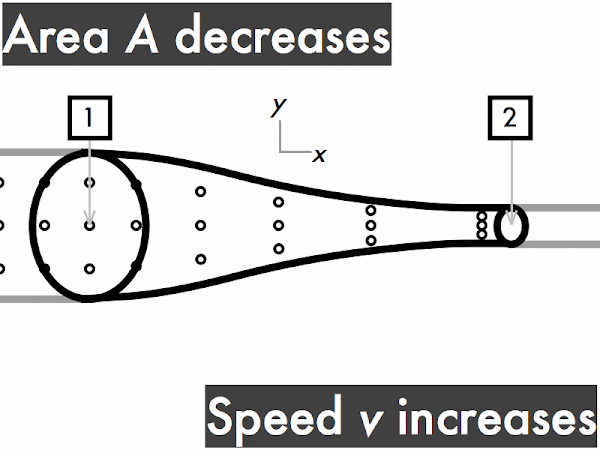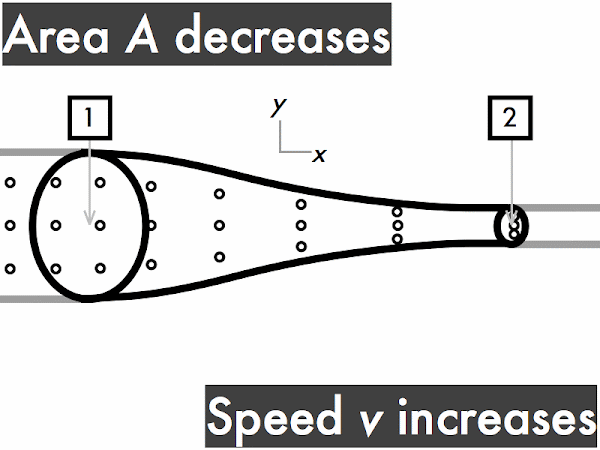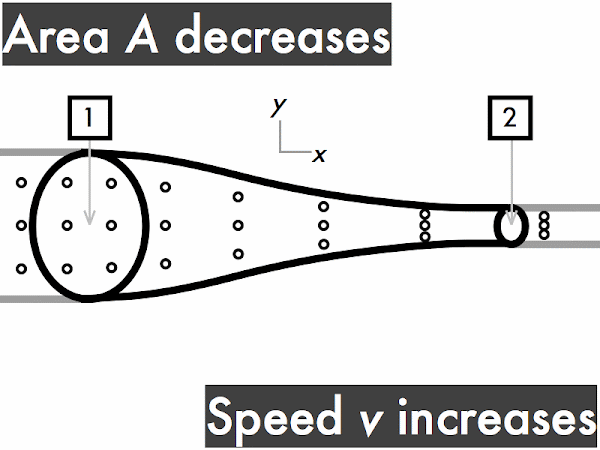
Conversely, for a pipe with decreasing cross-sectional area, the speed of the fluid through this pipe must have a corresponding increase, such that it flows more quickly through the narrow portion of the tube.

The second conservation law for ideal fluid flow follows from its laminar, non-viscous nature, as energy per volume density will be conserved if there are no losses to dissipative turbulence and frictional losses. (Incompressibility matters here too, such that the volume term in the energy per volume will be conserved.)

Bernoulli's equation is the extension of the static fluid relationship between pressure and gravitational potential energy per volume changes, to ideal fluid flow, with the addition of a translational kinetic energy per volume term. All three terms have equivalent units of Pa or J/m³, such that they can transfer to/from each other, as long as the net balance of exchanges is zero.

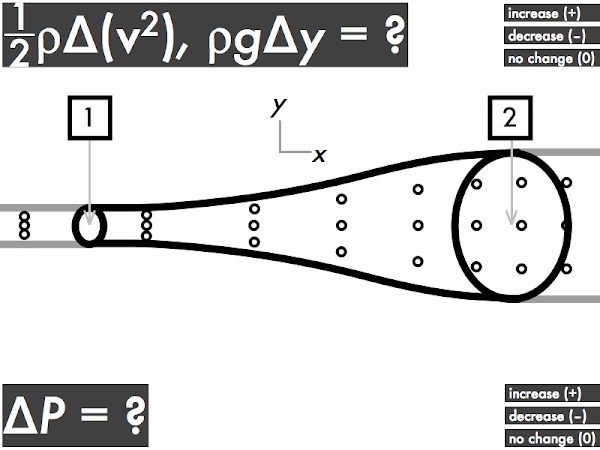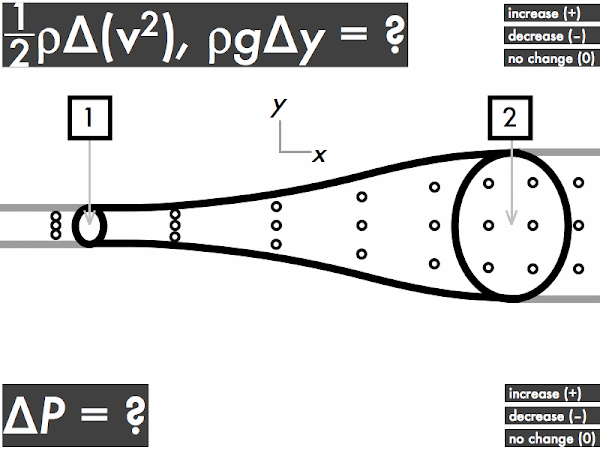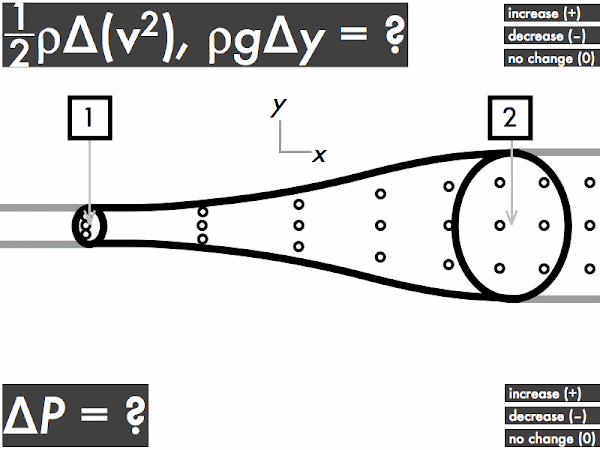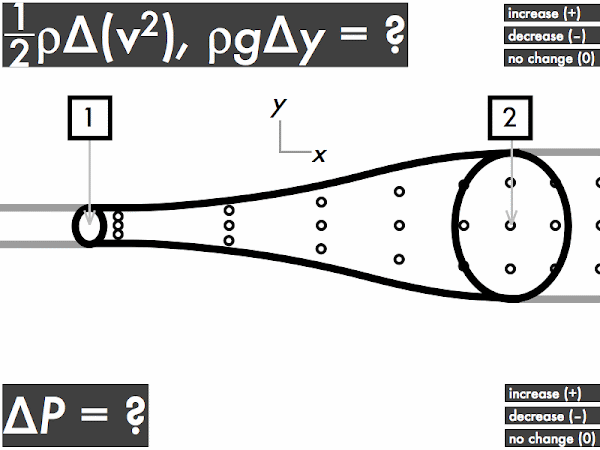
For an ideal fluid flowing through a horizontal pipe with a widening cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? Let's refer back to the continuity equation discussion above and recall that while the volume flow rate doesn't change, the speed changes, where the fluid slows down travels through this pipe. This means that the kinetic energy density will decrease (as it depends on the square of the speed), and this term will be negative.

Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change? Since the center of the pipe has no change in height (even though the cross-sectional areas are different, they are still "horizontally aligned" with each other), there is no change in the gravitational potential energy density term, and this term will be zero.

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change? Note the steps in determining the changes (if any) in pressure for this ideal flowing fluid--first we apply the continuity equation to determine the change in speeds (if any), which tells us the change (if any) in the kinetic energy density. We then look at the change in height of the centerline of the pipe (if any), which tells us the change (if any) in the gravitational potential energy density. Then we can look at Bernoulli's equation:

0 = ∆P + ρ·g·∆y + (1/2)·ρ·∆(v²),

and look at the increases (+) or decreases (–) (or no changes) of the terms we know so far:

0 = ∆P + (0) + (–).

In order to balance out this equation to equal zero on the left-hand side, the pressure of the fluid as it flows through this pipe must increase, making ∆P positive, such that:

0 = (+) + (0) + (–),

and both sides of Bernoulli's equation are balanced. So for this ideal fluid flowing through this widening pipe, the pressure will increase. This is why a weakened, enlarged blood vessel (an aneurysm) is dangerous, as blood flowing through this damaged, wider section will temporarily experience an increase in pressure as it slows down, and may widen the blood vessel even more and cause it to eventually rupture.

For an ideal fluid flowing through a horizontal pipe with a narrowing cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? (Refer back to the continuity equation discussion to determine this.) Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change?

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change?

(Note that the pressure should decrease in the narrow portion of this pipe, which is why the crimped hose at the start of this presentation collapsed--as air flowed through the narrow crimped portion of the hose, its speed increased, which made the pressure decrease inside the hose, and the surrounding atmospheric pressure then flattened the crimped portion even further.)

For an ideal fluid flowing through a descending horizontal pipe with a constant cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? (Refer back to the continuity equation discussion to determine this.) Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change?

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change?

Online reading assignment: fusion, nebulae, star cluster ages (SLO campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on fusion, nebulae, and star cluster ages.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"Hydrostatic equilibrium--I like the cheerleading analogy because it helped me understand the main concept."

"The 'House Party' model was a pretty clever way to describe stars and their turnoff points."

"There are only three colors emitted by nebulas."

"Fusion was interesting to me because I drive a Ford Fusion."

"Smaller stars will live longer...what? I would have thought that bigger stars would live longer."

"How much the pressure can differ from a large star to a small star. also found it interesting how much pressure and heat have to do with fusion."

"How stars can take hydrogen and change it into helium and energy! Just blows my mind, plus how these elements are made, making planets and life. Never thought of it this way."

"The process of nuclear fusion is interesting because it's where all elements in the universe originate. We're all stardust, man."

"The way an emission nebula works is the same way a neon light works...wow, mind blown!"

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"Turn-off points confused me very much. I had trouble comparing the 'house party' model to it."

"Hydrogen fusion deeply confuses me. Everything about it. The words are hard to understand and the concepts just don't click with me."

"The mass-luminosity relation because I don't understand it."

"As stars leave the main sequence category, does that mean they die? Since all of their hydrogen in their cores leave when leaving the main sequence then what happens? Just made me ponder while reading the section."

"Telling which nebula is which is confusing because I mix up colors a lot."

"What created the interstellar medium and how is it possible for it to form into a star?"

Fusion requires high temperatures in order for nuclei to move quickly enough to:

break heavy elements apart.	** [2]
create convection currents.	* [1]
overcome gravity.	*** [3]
overcome repulsion.	************************** [26]
(Unsure/guessing/lost/help!)	*** [3]

Briefly explain why "cold fusion" (producing energy from hydrogen fusion at room temperature) would be implausible.

"Under low pressures and temperatures, hydrogen does not get squeezed very much, and moves slowly, they won't collide with each other very much, or not at all. Not much squeezed, not much energy produced."

"In order for hydrogen fusion to work the protons need a lot of energy so that they move so fast they crash into each other and create energy. A room temperature atmosphere would not produce the need amount of energy."

"I don't understand the fusion section. please help."

"Because it needs heat, not cold."

Rank the fusion rates of these main-sequence stars (1 = fastest, 3 = slowest). (There are no ties.)
(Only correct responses shown.)

Low mass (red dwarf): slowest fusion rate [91%]
Medium-mass (sunlike): medium fusion rate [97%]
Massive: fastest fusion rate [89%]

Match the three different types of nebulae with their colors.
(Only correct responses shown.)

Emission: pink [80%]
Reflection: blue [83%]
Dark: brown/black [91%]

Match the three different types of nebulae with their composition.
(Only correct responses shown.)

Emission: hydrogen [91%]
Reflection: small dust particles [89%]
Dark: large dust particles [94%]

If there was an open invitation to a house party (no specific time given), when would you show up?

Early, or on time.	****** [6]
When the most people should be there.	****************************[28]
After most everyone has left.	* [1]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"So what time is the house party? When would you show up to the party? Or does the party not start until P-dog arrives?"

When are we going to look through the telescope at the Bowen Observatory again?" (Next week, after the end of class. Weather permitting.)

"What are you doing for Halloween?" (Already done.)

Online reading assignment: static fluids

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on static fluids.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"Pressure is described as the amount of force exerted over a certain area on a surface. In regards to fluids, it can also be described as energy per unit volume. The energy density conservation equation is the sum of the change in pressure and the gravitational energy per unit volume. As one increases, the other decreases to balance the total to 0."

"Pressure is equal to force/area: it is an inverse relationship because if there is more area and the same amount of force, the pressure will be less because there will be more area for the force to push on."

"Pressure can be considered as the amount of force exerted over a certain area on a surface. It also makes sense that if you don't wear snowshoes, the force of your weight, distributed over the area of your feet will create a pressure that cannot be supported by snow and your feet will sink in."

"To calculate buoyancy of an object you only use the volume of the object that is submerged, so if whole object is under water than you use volume of the whole object."

"Pressure can be interpreted as force/area or energy/volume. The buoyant force on an object depends on the density ρ of the fluid, and the volume of the object that is actually submerged in the fluid."

"Forces in a container are under pressure because the molecules are contently moving even if the fluid is static. The buoyant force is basically like the normal force of water on an object."

"Pressure in air or water increases as you go down and decreases as you go up. This is what makes your ears pop underwater or in high elevations."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"No idea how to calculate buoyant force."

"Why does something that is almost weightless like air cause pressure at all?"

"Not super sure yet how we are gonna use pressure as a form of energy (density)."

"All of these new terms are definitely fresh, more exposure to them will help."

"In the case of the ascending weather balloon popping I'm not sure if the pressure inside increased or the outside."

What is the numerical value for atmospheric pressure (P_atm, at sea level), in units of Pa?

"101,325 Pa."

"101.3 kPa = 1.013×10⁵ Pa."

"1."

"Honestly, I just didn't get to it (yet)."

To three significant digits, what is the numerical value for the density of water, in units of kg/m³?

"1.00×10³ kg/m³."

"999 kg/m³."

"1.00 kg/m³."

10,001.8 kg/m³."

"idk"

To two significant digits, what is the numerical value for the density of air (at 20° C), in units of kg/m³?

"1.2 kg/m³."

"1.2041 kg/m³."

"0.0012 kg/m³."

"idk"

For the air pressure surrounding the balloon as it rises from ground level to the upper atmosphere, indicate the changes in each of the energy density forms of the atmosphere.
(Only correct responses shown.)

ρ_air·g·∆y: increases [48%]
∆P: decreases [46%]

For the water pressure that surrounded these cups as they were taken deep underwater, indicate the changes in each of the energy density forms of the water.
(Only correct responses shown.)

ρ_water·g·∆y: decreases [43%]
∆P: increases [72%]

For the submerged diver floating underwater, Newton's __________ law applies, and the (downwards) weight force and (upwards) buoyant force on the diver are __________.

first; balanced.	**************************************** [40]
second; unbalanced.	**************** [16]
(Unsure/lost/guessing/help!)	** [2]

For the red ship (barely) afloat, Newton's __________ law applies, and its (downwards) weight force, the (downwards) oil platform's weight force, and the (upwards) buoyant force on the red ship are __________.

first; balanced.	******************************** [32]
second; unbalanced.	********************** [22]
(Unsure/lost/guessing/help!)	**** [4]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Could we focus more directly on the math for this lecture?" (Sure, but I think we need to clear up a lot of definitions and concepts first.)

"Only six weeks of class left until finals?" (Whuuuuuuut?)

"I need time to think more about all this." (There are only six weeks of class left until finals!)

"I will learn this." (Yes. Yes, you can.)

"What is the class' average grade?" (Two weeks ago, just after the first midterm scores were posted, the average student total score was just under the "C/B" cutoff. But you're all going to improve your studying, after making your keep-quit-start resolutions, right? Right?)

I'm confused by everything in the book. I do not like that book. At all. My magnitude of happiness with that book is not large."

Online reading assignment: fusion, nebulae, star cluster ages (NC campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on fusion, nebulae, and star cluster ages.

Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"The fusion process--I think it is interesting to know what causes the heat and light from the stars."

"Mst stars are born at the same time but age differently."

"Stars have automatic pressure-temperature thermostats. These are used to regulate temperature and pressure so the star can maintain stability. I find this process really crazy!"

"Smaller stars will live longer because they conserve their fuel better. I would have thought that bigger stars would live longer."

"Nebulae between stars could create more stars itself."

"Pink clouds = hydrogen :)"

"Hydrogen is squished together to form helium, I had no idea this was possible."

"Different nebulae always appear as certain colors."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"Hydrostatic equilibrium."

"Cold fusion."

"How mass could be formed into a star from the interstellar medium. What created the interstellar medium and how is it possible for it to form into a star? This was confusing because as I learn about astronomy many explanations for interesting things are vague or left out altogether making it confusing."

Fusion requires high temperatures in order for nuclei to move quickly enough to:

break heavy elements apart.	****** [6]
create convection currents.	**** [4]
overcome gravity.	*** [3]
overcome repulsion.	****************** [18]
(Unsure/guessing/lost/help!)	[0]

Briefly explain why "cold fusion" (producing energy from hydrogen fusion at room temperature) would be implausible.

"The gas must be very hot in order for the nuclei to have violent collisions and overcome the Coulomb barrier (repulsion), therefore room temperature would be implausible."

"Atoms all hate each other so the only way to make them collide and fuse to heat them up to millions of degrees so they're going so fast they don't notice before it's too late. They don't actually hate each other the charges of atomic nuclei just naturally repel other nuclei cause they're both mostly positive."

"The amount of energy required for fusion to occur would indefinitely raise the temperature, there is no way around it."

Rank the fusion rates of these main-sequence stars (1 = fastest, 3 = slowest). (There are no ties.)
(Only correct responses shown.)

Low mass (red dwarf): slowest fusion rate [77%]
Medium-mass (sunlike): medium fusion rate [87%]
Massive: fastest fusion rate [74%]

Match the three different types of nebulae with their colors.
(Only correct responses shown.)

Emission: pink [81%]
Reflection: blue [77%]
Dark: brown/black [90%]

Match the three different types of nebulae with their composition.
(Only correct responses shown.)

Emission: hydrogen [87%]
Reflection: small dust particles [84%]
Dark: large dust particles [84%]

If there was an open invitation to a house party (no specific time given), when would you show up?

Early, or on time.	****** [6]
When the most people should be there.	************************* [25]
After most everyone has left.	[0]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"I realize that the sun fuses four hydrogen nuclei to make one helium nucleus, but why does some mass 'vanish' in the process? Also where does it go?"(Albert Einstein's E = m·c² equation says that you can convert mass into energy; since the helium nucleus has less slightly mass than the four hydrogen nuclei used to build it, the energy released from this process came from the mass that 'vanished!')

"Are you throwing a house party? I'll bring cookies."

"So, was Mrs. P-dog a cheerleader?" (Yes. In my dreams.)

Online reading assignment: rotational dynamics

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on rotational dynamics.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"Rotational kinetic energy is being added to the energy transfer equation."

"How rolling objects combine rotational kinetic energy with translational kinetic energy as they move."

"I takes the place of mass and ω takes place of speed in rotational kinetic energy. This creates a formula that is similar to translational kinetic energy but only with the m and v swapped out."

"A rolling object's translational speed v and angular speed ω are constrained via the "rolling without slipping" condition v = r·ω, so an object with a radius r that has a slow or fast translational speed must also be rolling with a corresponding slow or fast angular speed."

"That translational kinetic energy and rotational kinetic energy are different. I got that much."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I was not particularly confused by anything in the reading."

"Rotational kinetic energy and determining if it is increasing or decreasing. And how to calculate rotational inertia."

"'For an object with both translational motion and rotational motion, it will have both translational kinetic energy and rotational kinetic energy'--I believe this concept needs a little more explanation before it sinks in."

"What is the lower-case Greek letter ω stand for? Does it stand for the rotational speed or something else?"

"When the different types of energy are increasing or decreasing. Can we go over examples of when each energy increases and decrease?"

"Rotational inertia--there are many different formulas for the different objects and I don't fully understand how to apply them in problems."

What is the SI (Système International) unit for rotational kinetic energy?

"J."

"kg·m²."

"rad/s²."

"I."

"K_rot."

"N/v."

Describe an object that only has rotational kinetic energy, and no translational kinetic energy.

"A hamster wheel."

"A wind turbine or a fan has no translational kinetic energy, as it is fixed to a central axis that is stationary."

"A Ferris Wheel."

"Toilet paper dispenser."

"Any object that is spinning, but not moving."

"A CD spinning in a CD player."

Describe an object that has both translational kinetic energy and rotational kinetic energy.

"Ball rolling down a hill."

"The boulder chasing Indiana Jones."

"A wheel on a car."

"A unicycle, which is spinning and moving."

"The tire rolling down the ski jump?"

"A bicycle."

From starting at the top of the ramp to the bottom of the ramp, indicate the changes in each of the energy forms of the tire.
(Only correct responses shown.)

Gravitational potential energy: decreases [78%]
Translational kinetic energy: increases [62%]
Rotational kinetic energy: increases [91%]

From starting at the top of the ramp to the bottom of the ramp, the energy form that experienced the greatest amount of change (increase or decrease) was the tire's:

gravitational potential energy.	***************** [17]
translational kinetic energy.	** [2]
rotational kinetic energy.	************** [14]
(There is a tie.)	**************** [16]
(Unsure/lost/guessing/help!)	****** [6]

For the subsequent part of this stunt, from starting at the bottom of the second ramp to reaching the top of its trajectory, indicate the changes in each of the energy forms of the tire.
(Only correct responses shown.)

Gravitational potential energy: increases [76%]
Translational kinetic energy: decreases [40%]
Rotational kinetic energy: no change [33%]

For the subsequent part of this stunt, from starting at the bottom of the second ramp to reaching the top of its trajectory, the energy form that experienced the greatest amount of change (increase or decrease) was the tire's:

gravitational potential energy.	***************************** [29]
translational kinetic energy.	**** [4]
rotational kinetic energy.	**** [4]
(There is a tie.)	************ [12]
(Unsure/lost/guessing/help!)	****** [6]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Why does my spell check say 'translational' is not a word?"

"How is the rotational kinetic energy affected when the tire is in the air? Does it still meet that 'no slipping' requirement from before?" (No, it does not--which means that the angular speed of the tire will ideally be constant, even though the translational speed changes as it would for projectile motion.)

"Why do you not include any mathematical examples of the ideas in the blogs?" (That's what the textbook is for. The blog presentations are to emphasize the important concepts over the extraneous topics in the textbook that will not appear on quizzes and exams.)

"Can we go over specific examples for each type of energy showing when each energy increases and decrease? Examples using the rotational and translational equations would be helpful." (Yes, as time allows. Don't take too long with the "scratcher" group quiz.)

"I'm coming to class!!!!" (Uh, okay.)

Physics presentation: static fluids

In this scene from Man from Atlantis, Mark Harris (played by Patrick Duffy) is put into a water pressure chamber that simulates different depths, and watches as test canisters are crushed by pressures equivalent to 20,000 ft, 25,000 ft, and 30,000 ft below sea level.

On a more reality-based aside, consider tourists who float in the high salinity waters of the Dead Sea.

We'll discuss these two different aspects of static fluids here: pressure, and buoyancy.

First, pressure--as a force per unit area density, then reinterpreted as a pressure per unit area density.

Pressure can be consider as the amount of force exerted over a certain area on a surface, whether by a macroscopic object, or by the random bombardment by atoms/molecules of gases or liquids. If you don't wear snowshoes, the force of your weight, distributed over the area of your feet will create a pressure that cannot be supported by soft, unpacked snow, and your feet will sink in.

However, the force of your weight distributed over a much larger snowshoe area will reduce the pressure exerted on the snow, and you will not sink in much, if at all.

From the definition of pressure as a force per area density, the unit of pressure is pascals (Pa), equivalent to N/m².

A more useful interpretation of pressure, especially in regards to fluids (gases and liquids) is to think of it as an energy per unit volume. Notice how the units of pascals equals N/m², and when both numerator and denominator by are multiplied by meters (m), these units become N/m² = (N·m)/(m³) = J/m³.

By interpreting pressure as a form of energy per unit volume, we can connect it to gravitational potential energy per unit volume ∆U_grav/V = m·g·∆y/V = (m/V)·g·∆y = ρ·g·∆y, which also has units of J/m³.

Pressure and gravitational potential energy per unit volume are then terms in an energy density "conservation" equation, and they are allowed to "exchange" Pa provided the fluid is static and there is no external work being put in or taken out of the fluid. In this form, then by picking two locations in the same static fluid, an increase or decrease in the ρ·g·∆y must have a corresponding decrease or increase in pressure (∆P).

A weather balloon that is partially filled at ground level will rise, and will seemingly inflate and eventually explode at very high elevations.

To explain what's going on here, we are going to analyze the static fluid that exists at both ground level and at a higher elevation: the air surrounding the balloon (i.e., the entire atmosphere), and not the contents of the balloon, which do not simultaneously exist at both locations (as it is "transported," and technically not a "static" fluid.)

Let's compare the air surrounding the balloon at ground level, and compare it to the air at the final higher elevation. Since the gravitational potential energy density depends on elevation, as the elevation of the balloon increases, the gravitational potential energy density of the surrounding air increases.

Looking at the energy density "conservation" equation for static fluids:

0 = ΔP + ρ·g·∆y,

Since the gravitational potential energy density of the air surrounding the balloon increases as it moves to higher elevations, then ρ·g·∆y is positive. In order to balance out this equation to equal zero on the left-hand side, the pressure of the air surrounding the balloon must have a corresponding decrease, making ΔP negative, such that:

0 = (–) + (+),

meaning that there is more air pressure at ground level than at a higher elevation. Essentially the pressure within the balloon remains constant, and because it is surrounded with lower pressure air at a higher elevation, the balloon will expand in size, and eventually "pop."

Notice the full-sized Styrofoam™ cup in the back, compared to other cups that were carried in the outside storage compartment of a submarine, where the air pockets inside these cups were collapsed by the surrounding water, effectively permanently shrinking the sizes of these cups. During this process, did the ρ·g·∆y increase or decrease? Did the water pressure surrounding the cups increase or decrease?

Second, buoyancy.

The buoyant force on an object depends on the density ρ of the fluid, and the volume of the object that is actually submerged in the fluid. While this is a simple definition, knowing the appropriate amount of volume to use in this equation is key to understanding buoyancy.

For a fully-submerged object, the volume used in calculating the buoyant force is the volume of the entire object, such that the buoyant force is given by:

F_B = ρ·g·V,

where ρ is the density of the surrounding fluid (water), and volume V is the entire volume of the diver, as he is fully submerged.

Here, since the object (the submerged diver) is floating underwater, Newton's first law applies, and the downwards weight force and the upwards buoyant force balance out.

For a partially-submerged object like this red ship, the volume used in calculating the buoyant force is not the volume of the entire object, but only the portion of the object that is actually submerged.

For the red ship, which Newton's law applies to its motion? How do the magnitudes of the downwards weight force and the upwards buoyant force compare? What fluid density should be put into the ρ in the buoyant force calculation?

Online reading assignment question: keep, quit, start

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

"2014-07-Phys205A-keep+.png"
http://flic.kr/p/pwoPrn
Originally uploaded by Waifer X

Wordle.net tag cloud for "keep" resolutions generated by responses from Physics 205A students at Cuesta College, San Luis Obispo, CA, fall semester 2014 (http://www.wordle.net/show/wrdl/8261739/Untitled).


"2014-07-Phys205A-quit+.png"
http://flic.kr/p/pNQ8zZ
Originally uploaded by Waifer X

Wordle.net tag cloud for "quit" resolutions generated by responses from Physics 205A students at Cuesta College, San Luis Obispo, CA, fall semester 2014 (http://www.wordle.net/show/wrdl/8261741/Untitled).


< "2014-07-Phys205A-start+.png"
http://flic.kr/p/pLJFdo
Originally uploaded by Waifer X

Wordle.net tag cloud for "start" resolutions generated by responses from Physics 205A students at Cuesta College, San Luis Obispo, CA, fall semester 2014 (http://www.wordle.net/show/wrdl/8261743/Untitled).

Students were asked to answer a "keep-quit-start" online reflection (hosted by SurveyMonkey.com) on their studying strategies/pitfalls (Mubayiwa, 2009).

Enter a word or brief phrase that describes what you intend to keep doing to study for this class. Explain your answer to the above question (what you intend to keep doing to study for this class).

Enter a word or brief phrase that describes what you intend to quit doing to study for this class. Explain your answer to the above question (what you intend to quit doing to study for this class).

Enter a word or brief phrase that describes what you intend to start doing to study for this class. Explain your answer to the above question (what you intend to start doing to study for this class).

[Word tags have been edited to consolidate related common subjects; student explanations are verbatim.]

Keep word tags:

askquestions
      ask questions to where i can see an example of each incident and be able to solve that problem.
      Get ready to know me well. Im gonna be asking a lot of questions.

everything
      I need to keep up with the reading assignments, homework problems, and coming to class so I can obtain as much point as I can to make up for my low midterm score.
      The reading is difficult a lot of the time I don't understand until you clarify. The homework enforces what you do in class but I have better success when you lecture first before I attempt the homework. The flash card questions are similar to quiz questions.
      I need to keep taking notes in lecture and keep doing the homework as well as start studying more and possibly getting outside help.
      Doing the extra credit, reading and homework assignment. Attention in the class. Working on problem and asking for confusion.

gettinglucky
      Well I don't know what I did, other than the questions seemed to line up with what I know. Hopefully this keeps happening for a while longer.

gotoclass
      Honestly, I struggle with this particular textbook- I don't find it to be very well laid out in terms of definitions, mathematical relationships, and examples in comparison to other science texts I've had. So, coming to class has been my main method of getting exposure to concepts.
      I can't succeed if I don't attend in the first place.
      I should keep going to class because the practice problems given during class time are helpful.
      I intend to KEEP coming to class consistently so that I absorb material from the lecture and examples, and so that I can take advantage of peer learning offered in class.
      I intend to keep going to class to reinforce the ideas and topics discussed in the book.
      I find the blog and the textbook interesting, but for me most of the knowledge I have picked up in this class has come from notes. There is something about visually seeing an explanation that makes a difference. Also having peers to converse with helps me sort out confusion.
      I've only missed one class and I intend to keep it that way, I know that if I miss a class I will have no idea what is going on, plus the book really isn't that helpful so its not like I can even read about it and catch up.
      I plan on attending every class possible to maximize participation points and get good example problems.
      continue to come to class every class
      It is helpful to see examples worked out on the board, and to get a little bit of exposure to the concepts we are expected to know. I wish the textbook and online presentations were as easy to follow; usually lecture is the only time I feel like I have a slight grasp on things. When I'm left to my own, I end up getting a little confused and a lot frustrated. Since I have little to no experience with this subject, I often don't know where to begin or even what questions to ask. I need a little bit of guidance, and showing up to class is the only way I can get a little bit of direction.
      I need to keep coming to the lectures, because it clarifies what I don't understand, and answers my questions. Plus, I get points toward my grade when I come to class.

homework
      I need to remember to take the survey quizzes for the reading and Homework assignments. I have an alarm on my phone to remind me now.
      i intend to keep onto of the homework assignments to be able to understand the concepts learned in class and know how to solve a problem in real life.
      If I complete assignments like homework and labs, I will keep up points in the class and be exposed to the material for the class.

interacting
      Im going to keep interacting on the questions we get asked during the class and discuss with my peers

keepingup
      By not staying behind, I wont need to relearn everything before an exam or quiz. This wil highly help me succeed.
      I need to keep studying the material and stay on top of doing the homework and the reading assignments. There are lots of little assignments, but the little assignments add up to lots of points that help in the long run.
      Need to better manage my time and procrastinate less to have time to better understand the material. And keep doing my study groups.
      I've found if I plan ahead and accomplish the homework ahead of time I understand more in class.
      Keeping up with the pace in this class is crucial. By doing homework on time, not only I get the points but I also understand the basic concepts that build up for more complex concepts in the subsequent classes.
      I intend to keep doing the homework and showing up to class. I feel like showing up to class really helps me patch the holes of things I don't get to a point that I am very comfortable with the material. The homeworks are free points so I will try to keep it up.

memorizing
      Keep memorizing the formulas.

organize
      When I have things organized it helps me focus better. For instance grouping things such as notes for quizzes and notes for midterms, I know what to focus on instead of getting confused.

payattention
      I intend to keep paying close attention in class in order to understand the material.

perseverance
      Since day one of this class I have maintained a work ethic equivalent to an "A" student.
      I give my all to every homework assignment, every exam and each lab. I am motivated to learn and have an insatiable appetite for knowledge.
      Honestly just putting the time and brain cells into the class is what's given me the grade I have.
      As long as i put forth the effort I will do well in this class.
      I just need to keep putting the time in studying and working out problems.
      I need to keep at my study habits and not stray too far. Even pick up the pace of what I am already doing so that I can exceed my own expectations.
      I just need to keep up my study habits and effort and more A's will follow on my tests.

preview
      I find the online presentations that are put together very helpful. Especially after I have attended the lecture on the material. Reviewing for the midterm by reading these presentations was also very beneficial.
      Reading about topics before they are discussed in class has made learning the material much easier. Normally, it is stressful and pressuring because I feel as though that when I put down the book I am suppose to completely understand it. By reading ahead and knowing we are going to talk about it in depth the next day, I am much more comfortable with the way we learn. I intend to stay ahead by reading early enough in the week so that I can learn at a comfortable pace and be able to practice as much as needed.

reading
      I will keep reading and studying every chapter in the book. I will also keep paying close attention in class. I will also keep doing well in labs.
      I intend to keep reading the chapters before each class as I feel like it helps me understand the lectures and example questions the next day in class.

review
      I'm going to continue looking at the online materials and explanations to what we go over in class and examine why each subject is the way it is.
      I tend to look over my class notes before a quiz or midterm in order to remind myself of what we went over in the days/ weeks prior.

studying
      Studying and learning the material on my own as well as it being explained in the class keeps me successful.
      plan better study habits, keep getting the homework assignments done.
      Read all notes, assigned readings, blog posts and work out all assigned problems.
      i underestimated the midterm. I need to study, study, and study some more
      although my study level is low and i havent been reading much of the chapters, i have done some of it. i intend tom improve myself on this point
      For test one I studied for around 7 hours and ended up getting a 75/75. So if I can keep studying that hard, I should be able to keep succeeding on the tests, and therefor, in the class.
      The amount of time you invest in something such as school will appreciate exponentially.
      I need to keep on studying and even though I did not do as well as I thought I would on the midterm, I need to prepare for the next one and continue to study.
      I need to review what i learned with someone that knows physics on a regular basis.

tutoringsessions
      I have been struggling in this class even with some tutoring once or twice a week. My plan is to review physics every day for a little along with some tutoring. If i keep looking at it daily I think it will become more clear.
      I have gotten a tutor in order to help better explain what I am having trouble with in this class.
      Hopefully be going to the Tutor lab to see if someone who knows this stuff can help me through problems

understanding
      In this class I feel like it is really important for me to not just "do" the work, but take the time to comprehend what I am doing as I go along. That way when I get a question I have not had yet, I am able to figure it out on my own because I have understood what I learned previously and can figure it out.

Quit word tags:

anxiety
      When I show up for an exam, no matter how much I have prepared and studied, I "FREAK OUT" at the moment I am taking the exam. I am taking steps to overcome this unwanted condition. I am reading studies on the subject and speaking to friends and professionals.

distractions
      If you're able to maintain concentration on school work and not become distracted you'll be able to do much better in school.
      end my netflix account.

everything
      what ever i was doing before was not working.

frustration
      Again, being honest here- I also struggle with this flipped-class idea. I'm just a student who prefers to come to the traditional class where I'm lectured to- that's how I learn best, at least with science and math classes. I struggle with it because I find myself not knowing what questions to ask in lecture, or what I'm expected to know (compounded by the textbook's tendency to show a plethora of mathematical relationships and concepts I don't hear about in class), because I suddenly come to a class where were expected to be more autonomous. I guess I just have to deal with it and get it done.
      I really don't like feeling confused. And, thus far, I've been very confused by physics. It makes me very frustrated when I can't understand something, and it makes me want to quit. Although I haven't (and won't) quit, I have allowed myself to get frustrated and not push myself further to try to understand. So I'll quit letting myself get frustrated.

missinghomework
      I've often forgotten or had trouble finding homework surveys.
      I need to remember to do the hw assignments because those points add up.
      in the beginning of the course I had trouble accessing the survey monkey website and didn't become accustomed to doing the homework before every class.
      I had trouble accessing the survey monkey website in the beginning of the course and didn't become accustomed to doing the homework the night before class
      I have missed the last couple of reading assignments and homework questions just because i forgot about them. I need to stop that before it becomes a habit.
      Missing out on the key stuff. Not practicing enough for the the test.

notaskingquestions
      I would like to quit not asking for help when I don't understand the material. I am kind of shy and I don't like to ask questions in class.

nothing
      There is nothing in particular that I want to change because I am pretty happy with how the class is going so far.

notunderstanding
      I believe that what I have the most trouble with is fully understanding equations, and I need to get a better grasp on all of the equations.

procrastinating
      I have been procrastinating or forgetting to turn in assignments or finishing lab write up.
      i intend to stay on top of what is needed to be done in this class such as homework, lab reports, and studying for quiz/test
      i usually procatinate alot on my physics homework and studying because i have alot of units this semester. I tend to lag in the subject because i feel like i should do more in class studying.
      I wait a long time to finish writing my lab reports. I think it's best to do them as soon as possible after the lab while the material is still fresh in my mind.
      I need to QUIT procrastinating in order to have enough time to do my assignments and learn the material the way it is laid out for me. This is a difficult one to overcome, as I work 40 hours/week and my main study space at home is in the living room of my apartment.
      I often procrastinate and wait until the very last minute to do the reading. This hinders me from really mastering the concepts. I notice that I have the right general idea but I cannot elaborate on these concepts because I have not put enough time in to master them.
      on the last exam I let the HW slide because I was busy with work and other classes. I still managed a 96% but was kinda stressed the weekend before.
      I have micro biology lecture and lab on Tues so I read but not as well as I should plus I feel rushed. I think rushing causes me not to retain what I should
      Procrastination habits keep me up late and stress me out before big assignments.
      I have a pretty big problem with getting distracted and pushing stuff till the last minute. I need to stop doing that and just finish assignments when they are first assigned.
      I need to be up to date in all my work. I need to read more of the text and try to compare all to what i learned in lecture class.
      I intend to not procrastinate as much on my homework in this class because I think it would really benefit me to have actually finished the homework before we discuss it in the class (which is the way the class is designed anyway).
      I am a huge procrastinator and wait until the day before tests and quizzes to study. I believe that this is one reason I am not happy with my grade thus far.
      Stop waiting until the day before classes to look at the homework and reading.
      I notice that if I do not look at my physics homework and notes over the weekend is very hard to remember small details. I tend to do my monday homework last minute on sunday evening. I need to start doing a little bit daily with a lot of detail and taking my time not just flying through it. If i stop doing things last minute it will greatly help.
      I tend to procrastinate on my studying, so I am not as efficient as I could be when studying for quizzes and exams.
      I need to quit waiting til the last minute to do the homework and need to stay on top of the reading and re read it every once in a while to keep it fresh in my mind.
      Stop being lazy and study the ideas and concepts more.
      I need to quit putting this class on the backburner and start putting more time and effort into really understanding concepts
      Putting off work till the last minute hurt because I don't always have the needed time to learn something.
      It is easier to retain information for me if I have reviewed it long before class.
      Stop leaving physic work till the last possible minute.
      I tend to skip the reading assignments until after lecture. I find myself falling behind in class now, and I want to stop that habit.
      I need to buckle down, and do what I need to do to get stuff done
      Although i do get the work done, procrastinating is a problem of mine... it just causes unnecessary headaches.
      This is something I am dealing with right now. I seem to do less urgent tasks then do physics till the last minute. I regret not finishing Physics with the other professor. I believe I was doing fairly well and completing the assignments, but I decided to find a job and work and lets not forget that the world cup was on as well. I dwell on the past and hurts me to think back about past mistakes about life.
      I need to do homework with enough time to really understand what I am doing.
      I need to stop waiting until a couple days before a quiz or test to really bare down and study.
      When I am doing my homework or studying I can get easily side tracked. I need to keep focused on the task at hand.
      When I wait until the night before a homework assignment is due to complete it, I always rush through the practice problems. I want to quit doing that and begin completing them the night before so I can be thorough with my understanding.

skimming
      I intend to slow down and take more time on the reading material. That way I can have a better idea of what is going on in class.
      Sometimes I find myself skimming when reading the assigned chapters or problems. This doesn't help me fully understand some concepts and I end up going back to understand better, actually wasting time.
      Sometimes I'll skim a hw question that is too difficult for me.

slacking
      Yep. Double negative. I haven't studied for a quiz yet and got a pretty horrible score on one, which shouldn't matter much in the end since a few of them get dropped. But I'd like to quit taking the quizzes so lightly and start studying for them harder so I can rack up them points!
      I sometimes don't try during the reading assignments. I read, but some of the problem questions that require work I don't do. And I need to because they help with understanding the chapter more.
      I've been in summer mode, and my grades show it. I need to stop being lazy buckle down and focus on this class so I can do well.
      Im going to quit overlooking the flashcard questions given during class and treat them more as test questions when doing them
      overlooking the flashcards and actually doing them more in depth.

working
      Cut my work hors down to 20 so that I have more time for studying.

worrying
      I worry about my grade too much. Right now I don't really have to, so that should help.

Start word tags:

alternatives
      While I understand the benefit to this pseudo-flipped classroom idea, I do not have the time to teach myself physics. I need some of these concepts (the majority of which are brand new material) to be explained to me. Since lecture is primarily devoted to working out a few examples, and the textbook has been less than helpful, I need to start finding other sources. I know I could benefit more from this class if I knew which questions to ask. Teaching myself physics has proved unsuccessful thus far, so I need to start putting effort into finding alternate resources.
      I will start reading other physics textbooks. I tried it for one chapter, and it helped a lot to clarify some of the material. I do not like the textbook that we use for this class, so I will start reading some other ones in addition.

askquestions
      Im gonna bring in the flash cards, and quiz reviews to prepare for test and quizes.
      I do the homework and reading, but then don't ask questions about things that I find confusing or difficult. I need to start getting my questions answered
      I need to get help from you (the teacher) or from classmates when I do not grasp all the material. Even when I understand the concepts I should broaden my understanding by getting more help.
      I find that I have lots of questions, but I don't usually think of them until after the professor has moved on from the topic he was discussing. At that point, I don't want to stop the lecture to ask.

believing
      I work a full time job due to my financial situation. Its really hard to be keeping everything i learn in track. But I keep believing that if there is a Will, than there is a Way.

diligence
      Start being more diligent about when and how much I study.

earlier
      I intend to start today. I need to stop procrastinating everything in my school life. I think I'll start tomorrow.

everything
      Read the book more and more, not only do the homework problems, but other problems, and maybe get a tutor.

flashcardquestions ("peer instruction," "think-pair-share")
      I am going to more carefully examine the flashcard questions and work out each one to practice and get a better idea of what might be on the next quiz.

homework
      I will start doing every homework assignment and extra credit opportunity
      I will start doing every single homework assignment and extra credit opportunity. I will also start to study harder and put more time into the class.
      I intend to START placing more emphasis on completing the homework exercises thoroughly, so that I can gain a better understanding of the fundamental concepts being taught, and the mathematical side of working problems in physics.
      I will work to be better at finishing more homework assignments before the class time and also before my study group. I think having my homework complete FIRST would help me to have more worthy discussions instead of feeling confused by concepts others already understand and I do not yet.
      If you start doing the homework and applying the knowledge you learn from the book and lecture it can only aide you in understanding the principles of physics.
      I will start paying more attention to each hw problem.

keepingup
      Setting at least an hour of physics studying every day. This will allow me to me to keep things I have previously learned fresh in my head.
      I have to keep at it and not fall behind.
      I need to study earlier before a test and every day go back through it all, so instead of cramming I'll have it all down to the point of just review.
      i plan on staying ahead of my studies.

maketime
      I intend to start setting more time aside for physics homework and study time so i can do better on quizzes and exams.

moreproblems
      Up until now, I have mainly focused on the conceptual aspects of the class, to the point where my math and problem solving skills are falling behind.
      I need to start working through more practice problems as I feel like thats what im struggling with the modt.
      I think if I can work through these I learn more and I should send my answers to you for correction
      Doing practice problems helps get familiar with problems you see on the test. Doing more then assigned problems.
      Sometimes they're too complex/I'm too tired so I just give up. Perhaps I should try harder.
      I fell if i did more homework problems, i would of had more practice, and done better on the midterm.
      Working on previous problem and have mastery one the concept. To know complex Relations
      I have a whiteboard at home and I don't utilize it enough. I want to start drawing out these practice problems on my board every single time so that it will be illustrated in my head.

nothing
      Not really gonna change anything to be honest. I am happy with my grade and feel I am understanding all the material fine (except for one thing I totally missed on midterm, but I get it now!).

organizing
      I need to start making a schedule for my study time instead of just studying randomly though out the day. This will keep my procrastination down and give myself goals.
      buy a planner.

payattention
      I usually study the day before quizzes or exams but tend to not focus in class. I sometimes understand better by self teaching because it helps me organize things better in my head, but don't understand some things, so paying more attention during class would probably help.

proactive
      I intend to be more proactive by doing the reading earlier, taking more time to understand the concepts, and seeking help when I do not understand something.

readmore
      Need to start doing more of the reading and pull apart the conce9ts more to better understand them, the math ksnt difficult, but the concepts are what i struggle with.
      I know that I haven't done the reading to the level that I need to in order to understand everything that is going on. I also need to study the information week by week instead of waiting until right before a quiz/test
      I need to read all the pages for the chapters in the book that correspond to what we are learning.
      i need to start really reading the material instead of just skimming it and moving on to the homework
      Reading and understanding the material by myself
      read the book a second time after the lecture to better understand the material.

reviewnotes
      I think going over my notes will help me retain the information better and hopefully I will do better on the quizzes.

selfstarting
      Kind of building off what I just said, the "real world" expects people to be self-starters in a lot of lines of work, so I guess I can't complain too much about the flipped-class thing. I came into this class being kind of excited about physics, since a lot of my experience has been with chemistry I thought it'd be enlightening to learn about how objects I can actually see interact and all the rest- but I find myself disappointed by counter-intuitive concepts. I talked to my brother about it who is a mechanical engineer and he said from his experience only engineers seemed to enjoy physics when he was in school. So, if nothing else, becoming more autonomous with my learning could make other future schooling easier.

studybetter
      I find that going to places like the library helps me study more effectively

studygroup
      I've made a few friends in the class and we work well during lecture, but we should start meeting outside of class in order to study

studymore
      I need to spend more time with the material in general. Doing more practice problems.
      i generally don't feel the need to study but don't always get the best results so i will begin studying concepts i am not confident on
      i intend to work alot harder in the second part of the semster since i have been laging way too much in this specific course. i also skipped alot of the homework during the first part of the semester, which i did my best to catch up on before the midterm 1 however, it did not help much. now i will do it sequentially and try and understand all i do better insteadof rushing through it.
      I skim the book but I don't read in depth.
      I need to study more than I do right now and actually ask more questions in and out of class.
      need to start studying more and going over the material more. If i looked at the notes more often and just ran through them, that would be better than nothing as far as familiarizing myself better with the material and some of the equations.
      Working harder toward success in this class is starting to be important, because I am on the verge of an A, and I need to pick up the pace if I want to end up with an A in this class.

takenotes
      Take far more in class notes, and notes from the assigned reading and blog posts.
      I am probably going to start taking my own notes from the book as i read it.

tutorsessions
      I have signed with a tutor with the hope that it will help in overcoming the "Test Anxiety".
      I plan to start using my tutor to help me have more success with studying for this class.