Physics 205A Quiz 3, fall semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Comprehensive Problem 3.74(c)
A ball is kicked off the edge of a cliff with an initial speed of 18.0 m/s, 10.0° above the horizontal. Neglect air resistance. Choose up to be the +y direction. How long would it take for the ball to fall to the ground 22.0 m below?
(A) 1.82 s.
(B) 2.12 s.
(C) 2.24 s.
(D) 2.46 s.
Correct answer (highlight to unhide): (D)
The following quantities are given (or assumed to be known):
(x0 = 0),
(y0 = 0),
(t0 = 0 s),
y = –22.0 m,
ay = –9.80 m/s2,
where the initial horizontal and vertical velocity components of the initial velocity vector are:
v0x = (18.0 m/s)·cos(+10°) = +17.7 m/s,
v0y = (18.0 m/s)·sin(+10°) = +3.13 m/s.
So in the equations for projectile motion, the following quantities are unknown, or are to be explicitly solved for:
x = v0x·t,
vy - v0y = ay·t,
y = (1/2)·(vy + v0y)·t,
y = v0y·t + (1/2)·ay·(t)2,
vy2 - v0y2 = 2·ay·y.
With the unknown quantity t to be solved for appearing in the fourth equation, with all other quantities given (or assumed to be known), then it becomes a quadratic equation:
y = v0y·t + (1/2)·ay·(t)2,
0 = –y + v0y·t + (1/2)·ay·(t)2,
where the quadratic formula terms are "c" = –(–22.0 m) = +22.0 m; "b" = +3.13 m/s, and "a" = "–4.90 m/s2, resulting in the roots:
t = –1.82 s, +2.46 s,
of which the positive root (response (D)) is the sole realistic answer, given the initial conditions.
(Response (B) is the time t = sqrt(2·y/ay) it would take for the ball to fall to the ground if it were released from rest; response (A) is the time it would take for the ball to fall to the ground if it were thrown at an angle of 10.0° below the horizontal; while response (C) is merely –(y)/ay).
Student responses
Sections 70854, 70855
(A) : 7 students
(B) : 11 students
(C) : 13 students
(D) : 14 students
Success level: 37%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.73
20080930
20080929
Physics quiz question: semicircular path car
Physics 205A Quiz 3, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 3.32
[3.0 points.] Consider a car that travels halfway around a circle of radius 30 m in a time of 4.5 s at a constant speed. The initial velocity is in the –x direction and the final velocity is in the +x direction. What is the magnitude of the average velocity during these 4.5 s?
(A) 0 m/s.
(B) 6.7 m/s.
(C) 13 m/s.
(D) 21 m/s.
Correct answer: (C)
The definition of average velocity is displacement over time, of which displacement is the straight-line vector from the initial location to final location. In this case, the magnitude of the displacement is the diameter of the circle:
|v_ave| = |delta_r|/delta_t = diameter/delta_t.
Response (D) is the average speed, which is the distance traveled over time, of which distance traveled is half of the circumference. Response (B) is the radius over time.
Student responses
Sections 70854, 70855
(A) : 4 students
(B) : 13 students
(C) : 13 students
(D) : 15 students
"Difficulty level": 28%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.55
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 3.32
[3.0 points.] Consider a car that travels halfway around a circle of radius 30 m in a time of 4.5 s at a constant speed. The initial velocity is in the –x direction and the final velocity is in the +x direction. What is the magnitude of the average velocity during these 4.5 s?
(A) 0 m/s.
(B) 6.7 m/s.
(C) 13 m/s.
(D) 21 m/s.
Correct answer: (C)
The definition of average velocity is displacement over time, of which displacement is the straight-line vector from the initial location to final location. In this case, the magnitude of the displacement is the diameter of the circle:
|v_ave| = |delta_r|/delta_t = diameter/delta_t.
Response (D) is the average speed, which is the distance traveled over time, of which distance traveled is half of the circumference. Response (B) is the radius over time.
Student responses
Sections 70854, 70855
(A) : 4 students
(B) : 13 students
(C) : 13 students
(D) : 15 students
"Difficulty level": 28%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.55
20080928
Erasing slate: There is meaning...
 "There is meaning..." by Anonymous
"There is meaning..." by AnonymousSeptember 24, 2008
Cuesta College, San Luis Obispo, CA
Latest scribbling on the lift-and-erase slate in the hallway, outside the office door.
Labels:
erasing slate
20080927
Erasing slate: COOKEE (sic)
 "COOKEE (sic)" by Anonymous
"COOKEE (sic)" by AnonymousSeptember 15, 2008
Cuesta College, San Luis Obispo, CA
Latest scribbling on the lift-and-erase slate in the hallway, outside the office door.
Labels:
erasing slate
20080926
Physics clicker question: pressed-down book
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 4.51
Students were asked the following clicker questions (Classroom Performance System, einstruction.com) near the beginning of their learning cycle:
 Mass of book = 0.50 kg.
Mass of book = 0.50 kg.
Coefficient of static friction mu_s = 0.45.
Coefficient of kinetic friction mu_k = 0.40.
You push down on the book with a force of 1.0 N. The normal force of the table on the book has a magnitude of:
(A) 4.9 N.
(B) 1.0 N.
(C) 4.9 N – 1.0 N.
(D) 4.9 N + 1.0 N.
(E) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 3 students
(B) : 13 students
(C) : 2 students
(D) : 16 students
(E) : 4 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 5 students
(C) : 0 students
(D) : 32 students
(E) : 1 student
Correct answer: (D)
The book has the weight force of the Earth pulling down on it (4.9 N), the applied force (1.0 N) pushing down on it, and since Newton's first law applies, the normal force of the table pushing up on the book is 5.9 N in magnitude.
Pre- to post- peer-interaction gains:
pre-interaction correct = 42%
post-interaction correct = 84%
Hake, or normalized gain <g> = 72%
This question was asked in a previous semester (Fall 2007), but with students who were not adequately coached on the think-(pair)-share methodology.
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 4.51
Students were asked the following clicker questions (Classroom Performance System, einstruction.com) near the beginning of their learning cycle:
 Mass of book = 0.50 kg.
Mass of book = 0.50 kg.Coefficient of static friction mu_s = 0.45.
Coefficient of kinetic friction mu_k = 0.40.
You push down on the book with a force of 1.0 N. The normal force of the table on the book has a magnitude of:
(A) 4.9 N.
(B) 1.0 N.
(C) 4.9 N – 1.0 N.
(D) 4.9 N + 1.0 N.
(E) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 3 students
(B) : 13 students
(C) : 2 students
(D) : 16 students
(E) : 4 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 5 students
(C) : 0 students
(D) : 32 students
(E) : 1 student
Correct answer: (D)
The book has the weight force of the Earth pulling down on it (4.9 N), the applied force (1.0 N) pushing down on it, and since Newton's first law applies, the normal force of the table pushing up on the book is 5.9 N in magnitude.
Pre- to post- peer-interaction gains:
pre-interaction correct = 42%
post-interaction correct = 84%
Hake, or normalized gain <g> = 72%
This question was asked in a previous semester (Fall 2007), but with students who were not adequately coached on the think-(pair)-share methodology.
20080925
Physics clicker question: Newton's second law
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) near the beginning of their learning cycle, just after introducing Newton's laws flowcharts.
An object is accelerating at a constant rate in a certain direction. What can be said about the force(s) (if any) acting on it?
(A) The forces (if any) that act on the object add up to zero.
(B) The force(s) that act on the object add up to a (non-zero) net force.
(C) (Nothing can be determined about the forces acting on the object.)
(D) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 15 students
(B) : 23 students
(C) : 0 students
(D) : 1 student
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 39 students
(C) : 0 students
(D) : 0 students
Correct answer: (B)
The object is accelerating, which means that Newton's second law applies, meaning that the forces that act on the object add up to a non-zero net force.
Pre- to post- peer-interaction gains:
pre-interaction correct = 59%
post-interaction correct = 100%
Hake, or normalized gain <g> = 100%
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) near the beginning of their learning cycle, just after introducing Newton's laws flowcharts.
An object is accelerating at a constant rate in a certain direction. What can be said about the force(s) (if any) acting on it?
(A) The forces (if any) that act on the object add up to zero.
(B) The force(s) that act on the object add up to a (non-zero) net force.
(C) (Nothing can be determined about the forces acting on the object.)
(D) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 15 students
(B) : 23 students
(C) : 0 students
(D) : 1 student
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 39 students
(C) : 0 students
(D) : 0 students
Correct answer: (B)
The object is accelerating, which means that Newton's second law applies, meaning that the forces that act on the object add up to a non-zero net force.
Pre- to post- peer-interaction gains:
pre-interaction correct = 59%
post-interaction correct = 100%
Hake, or normalized gain <g> = 100%
20080924
Education research: preliminary feedback on clickers (Chemistry 210FL, Cuesta College, Fall Semester 2008)
At the start of Fall semester 2008, Cuesta College students taking Chemistry 210FL (introductory chemistry) at Cuesta College, San Luis Obispo, CA have begun use of clickers (Classroom Performance System, einstruction.com) during lecture.
During the fourth week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
During the fourth week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
Learning Resource SurveyThe following are all of the student responses to this question, verbatim and unedited.
Cuesta College
Chemistry 210FL Fall Semester 2008 sections 70337, 71810, 71813, 72093
(N = 52)
I. In order to receive credit for completing this survey,
first enter your first and last name below:
____
II. How much did each of the following aspects of the class help
your learning?
II.1 Lecture by instructor.
1. Strongly disagree 2 : **
2. Disagree 2 : **
3. Neutral 3 : ***
4. Agree 24 : ************************ [4.1 +/- 1.0]
5. Strongly agree 20 : ********************
II.2 Working in groups on FAL (Facilitated Assisted Learning) activities.
1. Strongly disagree 4 : ****
2. Disagree 2 : *******
3. Neutral 8 : ********
4. Agree 16 : **************** [4.0 +/- 1.3]
5. Strongly agree 22 : **********************
II.3 Using clickers to participate in class.
1. Strongly disagree 3 : ***
2. Disagree 5 : *****
3. Neutral 15 : ***************
4. Agree 20 : ******************** [3.5 +/- 1.1]
5. Strongly agree 9 : *********
II.4 Reading the textbook.
1. Strongly disagree 1 : *
2. Disagree 2 : **
3. Neutral 13 : *************
4. Agree 24 : ************************ [3.8 +/- 0.9]
5. Strongly agree 12 : ************
II.5 Demonstrations/videos in class.
1. Strongly disagree 1 : *
2. Disagree 2 : **
3. Neutral 28 : ****************************
4. Agree 10 : ********** [3.5 +/- 0.9]
5. Strongly agree 10 : **********
II.6 Interacting with other students during class.
1. Strongly disagree 1 : *
2. Disagree 3 : ***
3. Neutral 11 : ***********
4. Agree 23 : *********************** [3.9 +/- 0.9]
5. Strongly agree 14 : **************
II.7 Interacting with other students outside of class.
1. Strongly disagree 0 :
2. Disagree 4 : ****
3. Neutral 12 : ************
4. Agree 22 : ********************** [3.9 +/- 0.9]
5. Strongly agree 14 : **************
III. Answer the following statements which may or may not describe
your beliefs about the use of clickers in this class.
III.1 I like using clickers.
1. Strongly disagree 3 : ***
2. Disagree 5 : *****
3. Neutral 10 : **********
4. Agree 26 : ************************** [3.6 +/- 1.1]
5. Strongly agree 8 : ********
III.2 Clickers helped me understand lectures better.
1. Strongly disagree 3 : ***
2. Disagree 11 : ***********
3. Neutral 24 : ************************ [3.0 +/- 1.1]
4. Agree 9 : *********
5. Strongly agree 5 : *****
III.3 I would recommend using clickers in future semesters of this class.
1. Strongly disagree 1 : *
2. Disagree 6 : ******
3. Neutral 15 : ***************
4. Agree 22 : ********************** [3.6 +/- 0.9]
5. Strongly agree 8 : ********
III.4 I will avoid other classes using clickers in future semesters.
1. Strongly disagree 14 : **************
2. Disagree 28 : **************************** [2.0 +/- 2.0]
3. Neutral 9 : *********
4. Agree 0 :
5. Strongly agree 1 : *
III.5 Clickers were a positive experience.
1. Strongly disagree 1 : *
2. Disagree 7 : *******
3. Neutral 14 : **************
4. Agree 26 : ************************** [3.5 +/- 0.9]
5. Strongly agree 4 : ****
III.6 Too much time in class was spent using clickers.
1. Strongly disagree 7 : *******
2. Disagree 32 : ******************************** [2.2 +/- 1.2]
3. Neutral 9 : *********
4. Agree 2 : **
5. Strongly agree 2 : **
III.7 Too many clicker questions were asked.
1. Strongly disagree 10 : **********
2. Disagree 30 : ****************************** [2.1 +/- 1.5]
3. Neutral 10 : **********
4. Agree 2 : **
5. Strongly agree 0 :
III.8 Using clickers was difficult.
1. Strongly disagree 18 : ******************
2. Disagree 24 : ************************ [1.9 +/- 2.6]
3. Neutral 6 : ******
4. Agree 4 : ****
5. Strongly agree 0 :
IV. (Optional.) Please type in any comments you may have regarding
the use of clickers in Chemistry 210FL.
"Clickers are way too expensive especially if you are taking a class just as a prerequiste for another class that doesn't have a clicker."
"I thought the cost of the clicker which was $20 something and to register the clicker which was $14 was to much considering the text books where around $200. The actual using of the clicker in class was just ok for me."
"The clicker situation started off poorly. Problems with getting it going were detrimental but overall I think it is time beneficial over handing out quizes and gathering them. One problem is that I think they are "busy" work but understand that in the JC system it makes sense to require students to stay current."
"To expensive! I am a poor student and I was barely able to offord this product and its registration after buying the clickers and buyin all of my text-books for this classe. I thought the clickers were just an extra thing to spend money on. But, over all I can see some positive things using the Clickers. 1) It helps the teacher greading students on participation. 2) It helps some students who are shy to participate none-verbally in some of the classes activities. But,I still think it's to costly, since I don't have problems raising my hand to participate."
"Only one day so far did I have an issue getting the clicker to send my answers in and felt like I wasn't given enough time to submit "send" then answers. Still don't know if I got the credit for those questions that I completed correctly on paper."
"im more traditional with the paper and pen deal. i dont like the clickers to much but its ok"
"I think they work good and are lot easier that passing out papers. Then takin the time to collect them."
"not about clickers...just the FAL's are useless, a waste of time. Having them in a lab room is so uncomfortable with knees jammed in drawers, not helpful at all, not to mention a "facilitator" who doesn't seem sure of the answers herself. Nice person, but after the first week we don't even really seek her help. Also, I was often lost doing the FAL and then the next lecture would include what I needed to do the FAL that was already due. That was frustrating. Thanks for listening!"
"the only thing i didn't like about the clickers was when the professor changed part of some of the practice problems two minutes before she asked us to enter the CORRECT answer. if your going to assign problems for us to do, and we did the work you should keep it that way."
"The clickers were a good and fun way to learn the material. Just that when the system doesnt cooperate and haveing difficulties connecting to the recievers and loosing points because of the time limit. Overall on a scale 1-10 I give the clickers an 8"
"I REALLY FELT RUSHED THE FIRST TIME WE USED THEM. IT WAS DIFFICULT TO FIGURE EVERYTHING OUT AND THEN WE WERE BEING TIMED AND IT CAUSED ME TO PANIC AND MESS UP THE FIRST QUIZ."
"i like them but i wish that they weren't so expensive to use. maybe a class set may be possible next semester. Set it up for the students and have them buy them and register them under maybe student 1 or something. Take the initiative and every semester have the money go back to the students that purchased them before the new class. That way they are free for everyone. And you have a replacement plan in case someone wrecks one. I know that doesn't make a whole lot of sense but it makes a lot of sense in my head. Hope you can figure out the mess i just typed. haha"
"More time spent on mass, volume and density."
"Going "green" is always a good idea."
"The clickers are cool, it makes it easier to be involved in the class."
"Clickers were a waste of money both in upfront costs and subscription fees. The device itself is a good idea, but why does it have to be linked to an expensive subscription service? There has to be a more competitive option."
"I like the idea its very helpful"
"Sometimes the clickers are a little difficult, like in the begnining they didn't wok and we wasted lecture time, but other than that they are cool."
Labels:
clickers,
education research,
SALG
20080923
Astronomy clicker question: "exact change required"
Astronomy 210, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle:
A photon with slightly more energy than is required for an electron to move between energy levels 1 to 2 would:
(A) be absorbed, causing the electron to move between energy levels 1 to 2.
(B) not be absorbed, such that the electron stays in energy level 1.
(C) (Not enough information is given to answer this.)
(D) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 21 students
(B) : 4 students
(C) : 0 students
(D) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 16 students
(B) : 9 students
(C) : 1 student
(D) : 0 students
Correct answer: (B)
Some students latched on to the key phrase from the textbook: "exact change required." Most students had assumed (incorrectly) that the electron could "make change" and jump up to the higher orbital, and somehow dispose of the excess energy.
Pre- to post- peer-interaction gains:
pre-interaction correct = 16%
post-interaction correct = 35%
Hake (normalized) gain <g> = 22%
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle:
A photon with slightly more energy than is required for an electron to move between energy levels 1 to 2 would:
(A) be absorbed, causing the electron to move between energy levels 1 to 2.
(B) not be absorbed, such that the electron stays in energy level 1.
(C) (Not enough information is given to answer this.)
(D) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 21 students
(B) : 4 students
(C) : 0 students
(D) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 16 students
(B) : 9 students
(C) : 1 student
(D) : 0 students
Correct answer: (B)
Some students latched on to the key phrase from the textbook: "exact change required." Most students had assumed (incorrectly) that the electron could "make change" and jump up to the higher orbital, and somehow dispose of the excess energy.
Pre- to post- peer-interaction gains:
pre-interaction correct = 16%
post-interaction correct = 35%
Hake (normalized) gain <g> = 22%
20080922
Astronomy clicker question: interferometry
Astronomy 210, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle:
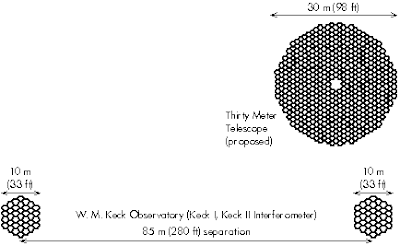
What disadvantage does the proposed Thirty Meter Telescope have, compared to the combination of the two W. M. Keck Observatory telescopes used as an interferometer?
(A) Light-gathering power.
(B) Resolving power.
(C) Magnifying power.
(D) (More than one of the above choices.)
(E) (None of the above choices.)
(F) (I'm lost, and don't know how to answer this.)
Section 70158
(A) : 12 students
(B) : 30 students
(C) : 10 students
(D) : 9 students
(E) : 4 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70158
(A) : 2 students
(B) : 51 students
(C) : 8 students
(D) : 2 students
(E) : 1 student
(F) : 1 student
Correct answer: (B)
Light-gathering power depends on the area of the primary mirror (or lens) of a telescope, while the resolving power depends on the diameter of the primary mirror, whether it is a single contiguous piece (as for the Thirty Meter Telescope), or separated components (as for the Keck Interferometer).
Pre- to post- peer-interaction gains:
pre-interaction correct = 46%
post-interaction correct = 78%
Hake (normalized) gain <g> = 60%
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle:

What disadvantage does the proposed Thirty Meter Telescope have, compared to the combination of the two W. M. Keck Observatory telescopes used as an interferometer?
(A) Light-gathering power.
(B) Resolving power.
(C) Magnifying power.
(D) (More than one of the above choices.)
(E) (None of the above choices.)
(F) (I'm lost, and don't know how to answer this.)
Section 70158
(A) : 12 students
(B) : 30 students
(C) : 10 students
(D) : 9 students
(E) : 4 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70158
(A) : 2 students
(B) : 51 students
(C) : 8 students
(D) : 2 students
(E) : 1 student
(F) : 1 student
Correct answer: (B)
Light-gathering power depends on the area of the primary mirror (or lens) of a telescope, while the resolving power depends on the diameter of the primary mirror, whether it is a single contiguous piece (as for the Thirty Meter Telescope), or separated components (as for the Keck Interferometer).
Pre- to post- peer-interaction gains:
pre-interaction correct = 46%
post-interaction correct = 78%
Hake (normalized) gain <g> = 60%
20080921
Astronomy quiz question: inferior planets at midnight
Astronomy 210 Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] Why are Mercury and Venus never visible in the San Luis Obispo, CA sky at midnight?
(A) Mercury and Venus never exhibit retrograde motion.
(B) Mercury and Venus are too small to reflect enough sunlight.
(C) The orbits of Mercury and Venus are smaller than the orbit of the Earth.
(D) Mercury and Venus cannot exhibit gibbous phases.
Correct answer: (C)
Since the orbits of Mercury and Venus are smaller than the orbit of the Earth (making them inferior planets), they can never appear behind the Earth, with respect to the Sun, and thus cannot be overhead (or anywhere in the sky) at midnight for typical temperate latitudes such as for San Luis Obispo, CA.
Student responses
Section 70158
(A) : 9 students
(B) : 3 students
(C) : 42 students
(D) : 4 students
"Difficulty level": 75%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.76
Cuesta College, San Luis Obispo, CA
[4.0 points.] Why are Mercury and Venus never visible in the San Luis Obispo, CA sky at midnight?
(A) Mercury and Venus never exhibit retrograde motion.
(B) Mercury and Venus are too small to reflect enough sunlight.
(C) The orbits of Mercury and Venus are smaller than the orbit of the Earth.
(D) Mercury and Venus cannot exhibit gibbous phases.
Correct answer: (C)
Since the orbits of Mercury and Venus are smaller than the orbit of the Earth (making them inferior planets), they can never appear behind the Earth, with respect to the Sun, and thus cannot be overhead (or anywhere in the sky) at midnight for typical temperate latitudes such as for San Luis Obispo, CA.
Student responses
Section 70158
(A) : 9 students
(B) : 3 students
(C) : 42 students
(D) : 4 students
"Difficulty level": 75%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.76
20080920
Astronomy quiz question: heliocentric model of retrograde motion
Astronomy 210 Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] How does Copernicus' model explain the retrograde motion of a planet?
(A) The only perfect shape is a circle, and the only perfect motion is uniform motion.
(B) A planet slows down in its orbit when it is further from the sun, and speeds up in its orbit when it is closer to the sun.
(C) A planet moves around a circle that itself moves along an orbit around the Earth.
(D) A planet has a different orbital distance and speed around the sun from the Earth's orbital distance and speed around the sun.
Correct answer: (D)
Copernicus' model of planetary motion explains retrograde motion as a "lapping illusion" when planets in different orbits traveling at different speeds move past each other. Response (A) is Ptolemy's model of retrograde motion; response (B) is Kepler's second law; response (C) is based on Aristotle's first principles, but does not explain retrograde motion.
Student responses
Section 70158
(A) : 9 students
(B) : 11 students
(C) : 14 students
(D) : 18 students
"Difficulty level": 39%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.35
Cuesta College, San Luis Obispo, CA
[4.0 points.] How does Copernicus' model explain the retrograde motion of a planet?
(A) The only perfect shape is a circle, and the only perfect motion is uniform motion.
(B) A planet slows down in its orbit when it is further from the sun, and speeds up in its orbit when it is closer to the sun.
(C) A planet moves around a circle that itself moves along an orbit around the Earth.
(D) A planet has a different orbital distance and speed around the sun from the Earth's orbital distance and speed around the sun.
Correct answer: (D)
Copernicus' model of planetary motion explains retrograde motion as a "lapping illusion" when planets in different orbits traveling at different speeds move past each other. Response (A) is Ptolemy's model of retrograde motion; response (B) is Kepler's second law; response (C) is based on Aristotle's first principles, but does not explain retrograde motion.
Student responses
Section 70158
(A) : 9 students
(B) : 11 students
(C) : 14 students
(D) : 18 students
"Difficulty level": 39%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.35
20080919
Astronomy quiz question: geocentric model of retrograde motion
Astronomy 210 Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] How does Ptolemy's model explain the retrograde motion of a planet?
(A) The only perfect shape is a circle, and the only perfect motion is uniform motion.
(B) A planet has a different orbital distance and speed around the sun from the Earth's orbital distance and speed around the sun.
(C) A planet moves around a circle that itself moves along an orbit around the Earth.
(D) A planet slows down in its orbit when it is further from the sun, and speeds up in its orbit when it is closer to the sun.
Correct answer: (C)
Ptolemy's model of planetary motion used epicycles moving along deferents to explain the retrograde loops of planets. Response (A) is based on his (and Aristotle's) first principles, but in and of itself is not a model of retrograde motion; response (B) is Copernicus' heliocentric explanation of retrograde motion; and response (D) is Kepler's second law.
Student responses
Section 70160
(A) : 1 student
(B) : 2 students
(C) : 22 students
(D) : 8 students
"Difficulty level": 69%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.89
Cuesta College, San Luis Obispo, CA
[4.0 points.] How does Ptolemy's model explain the retrograde motion of a planet?
(A) The only perfect shape is a circle, and the only perfect motion is uniform motion.
(B) A planet has a different orbital distance and speed around the sun from the Earth's orbital distance and speed around the sun.
(C) A planet moves around a circle that itself moves along an orbit around the Earth.
(D) A planet slows down in its orbit when it is further from the sun, and speeds up in its orbit when it is closer to the sun.
Correct answer: (C)
Ptolemy's model of planetary motion used epicycles moving along deferents to explain the retrograde loops of planets. Response (A) is based on his (and Aristotle's) first principles, but in and of itself is not a model of retrograde motion; response (B) is Copernicus' heliocentric explanation of retrograde motion; and response (D) is Kepler's second law.
Student responses
Section 70160
(A) : 1 student
(B) : 2 students
(C) : 22 students
(D) : 8 students
"Difficulty level": 69%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.89
20080918
Astronomy quiz question: in the penumbra of the Moon
Astronomy 210 Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] An observer is located on the surface of the Earth, and this observer is also located in the penumbra of the Moon. What type of eclipse is seen by the observer?
(A) A total lunar eclipse.
(B) A partial lunar eclipse.
(C) An annular solar eclipse.
(D) A partial solar eclipse.
(E) A total solar eclipse.
Correct answer: (D)
Assuming that the umbra of the Moon never does pass over the observer (for which this would be response (E), a total solar eclipse), this will be only a partial solar eclipse. If the observer were in the "negative shadow" of the Moon (out past the umbra), then an annular solar eclipse would be observed (response (C)). Responses (A) and (B) correspond to the Moon itself being in the umbra or penumbra of the Earth, respectively.
Student responses
Section 70160
(A) : 5 students
(B) : 10 students
(C) : 0 students
(D) : 15 students
(E) : 3 students
"Difficulty level": 51%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.78
Cuesta College, San Luis Obispo, CA
[4.0 points.] An observer is located on the surface of the Earth, and this observer is also located in the penumbra of the Moon. What type of eclipse is seen by the observer?
(A) A total lunar eclipse.
(B) A partial lunar eclipse.
(C) An annular solar eclipse.
(D) A partial solar eclipse.
(E) A total solar eclipse.
Correct answer: (D)
Assuming that the umbra of the Moon never does pass over the observer (for which this would be response (E), a total solar eclipse), this will be only a partial solar eclipse. If the observer were in the "negative shadow" of the Moon (out past the umbra), then an annular solar eclipse would be observed (response (C)). Responses (A) and (B) correspond to the Moon itself being in the umbra or penumbra of the Earth, respectively.
Student responses
Section 70160
(A) : 5 students
(B) : 10 students
(C) : 0 students
(D) : 15 students
(E) : 3 students
"Difficulty level": 51%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.78
Labels:
annular solar eclipse,
lunar eclipse,
Moon,
negative shadow,
penumbra,
solar eclipse,
Sun,
umbra
20080917
Physics clicker question: dropped and horizontally thrown balls
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Multiple-Choice Question 3.10
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle.
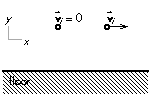 A ball is released from rest, at a certain height above a floor. At the same time, a ball is thrown from the same height above the floor, with an initial horizontal velocity. Which ball will hit the floor with the fastest speed?
A ball is released from rest, at a certain height above a floor. At the same time, a ball is thrown from the same height above the floor, with an initial horizontal velocity. Which ball will hit the floor with the fastest speed?
(A) The ball released from rest.
(B) The ball with an initial horizontal velocity.
(C) (There is a tie.)
(D) (Not enough information is given.)
(E) (I'm lost, and I don't know how to answer this.)
Sections 70854, 70855
(A) : 2 students
(B) : 25 students
(C) : 15 students
(D) : 2 students
(E) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 35 students
(C) : 9 students
(D) : 0 students
(E) : 8 students
Correct answer: (B)
Both balls will reach the ground at the same time, as discussed in a previous clicker question. During the whole-class discussion, students offered several explanations as to why the initial horizontal velocity ball would have a faster speed as it hits the ground: (i) its trajectory would carry it over a longer distance traveled, and thus must have a longer (average) speed over the time interval; (ii) its final velocity vector would have its original horizontal component in addition to its downwards vertical component.
Pre- to post- peer-interaction gains:
pre-interaction correct = 57%
post-interaction correct = 80%
Hake, or normalized gain <g> = 53%
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Multiple-Choice Question 3.10
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle.
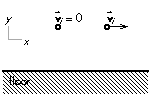 A ball is released from rest, at a certain height above a floor. At the same time, a ball is thrown from the same height above the floor, with an initial horizontal velocity. Which ball will hit the floor with the fastest speed?
A ball is released from rest, at a certain height above a floor. At the same time, a ball is thrown from the same height above the floor, with an initial horizontal velocity. Which ball will hit the floor with the fastest speed?(A) The ball released from rest.
(B) The ball with an initial horizontal velocity.
(C) (There is a tie.)
(D) (Not enough information is given.)
(E) (I'm lost, and I don't know how to answer this.)
Sections 70854, 70855
(A) : 2 students
(B) : 25 students
(C) : 15 students
(D) : 2 students
(E) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 35 students
(C) : 9 students
(D) : 0 students
(E) : 8 students
Correct answer: (B)
Both balls will reach the ground at the same time, as discussed in a previous clicker question. During the whole-class discussion, students offered several explanations as to why the initial horizontal velocity ball would have a faster speed as it hits the ground: (i) its trajectory would carry it over a longer distance traveled, and thus must have a longer (average) speed over the time interval; (ii) its final velocity vector would have its original horizontal component in addition to its downwards vertical component.
Pre- to post- peer-interaction gains:
pre-interaction correct = 57%
post-interaction correct = 80%
Hake, or normalized gain <g> = 53%
20080916
Education research: preliminary feedback on clickers (Cuesta College, Astronomy 210, Fall Semester 2008)
At the start of Fall semester 2008, Cuesta College students taking Astronomy 210 (introductory astronomy) at Cuesta College, San Luis Obispo, CA have begun use of clickers (Classroom Performance System, einstruction.com) to engage in peer-interaction ("think-(pair)-share") discussion questions during lecture.
During the third week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
During the third week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
Learning Resource SurveyThe following are all of the student responses to this question, verbatim and unedited.
Cuesta College
Astronomy 210 Fall Semester 2008 sections 70158, 70160
(N = 44)
I. In order to receive credit for completing this survey,
first enter your first and last name below:
____
II. How much did each of the following aspects of the class help
your learning?
II.1 Lecture by instructor.
1. Strongly disagree 0 :
2. Disagree 3 : ***
3. Neutral 9 : *********
4. Agree 18 : ****************** [4.0 +/- 0.9]
5. Strongly agree 14 : **************
II.2 Working in groups on in-class activities.
1. Strongly disagree 0 :
2. Disagree 2 : **
3. Neutral 3 : ***
4. Agree 23 : *********************** [4.2 +/- 0.8]
5. Strongly agree 16 : ****************
II.3 Using clickers to participate in class.
1. Strongly disagree 0 :
2. Disagree 1 : *
3. Neutral 6 : ******
4. Agree 21 : ********************* [4.2 +/- 0.7]
5. Strongly agree 16 : ****************
II.4 Reading the textbook.
1. Strongly disagree 0 :
2. Disagree 7 : *******
3. Neutral 17 : ***************** [3.4 +/- 0.9]
4. Agree 14 : **************
5. Strongly agree 6 : ******
II.5 Demonstrations/videos in class.
1. Strongly disagree 0 :
2. Disagree 2 : **
3. Neutral 4 : ****
4. Agree 21 : ********************* [4.1 +/- 0.8]
5. Strongly agree 15 : ***************
II.6 Interacting with other students during class.
1. Strongly disagree 0 :
2. Disagree 1 : *
3. Neutral 5 : *****
4. Agree 24 : ************************ [4.2 +/- 0.7]
5. Strongly agree 14 : **************
II.7 Interacting with other students outside of class.
1. Strongly disagree 3 : ***
2. Disagree 3 : ***
3. Neutral 27 : *************************** [3.1 +/- 0.9]
4. Agree 10 : **********
5. Strongly agree 1 : *
III. Answer the following statements which may or may not describe
your beliefs about the use of clickers in this class.
III.1 I like using clickers.
1. Strongly disagree 0 :
2. Disagree 0 :
3. Neutral 8 : ********
4. Agree 25 : ************************* [4.1 +/- 0.7]
5. Strongly agree 11 : ***********
III.2 Clickers helped me understand lectures better.
1. Strongly disagree 0 :
2. Disagree 2 : **
3. Neutral 13 : *************
4. Agree 21 : ********************* [3.8 +/- 0.8]
5. Strongly agree 8 : ********
III.3 I would recommend using clickers in future semesters of this class.
1. Strongly disagree 1 : *
2. Disagree 1 : *
3. Neutral 4 : ****
4. Agree 24 : ************************ [4.1 +/- 0.8]
5. Strongly agree 14 : **************
III.4 I will avoid other classes using clickers in future semesters.
1. Strongly disagree 16 : ****************
2. Disagree 24 : ************************ [1.8 +/- 2.5]
3. Neutral 2 : **
4. Agree 1 : *
5. Strongly agree 1 : *
III.5 Clickers were a positive experience.
1. Strongly disagree 0 :
2. Disagree 0 :
3. Neutral 6 : ******
4. Agree 26 : ************************** [4.1 +/- 0.6]
5. Strongly agree 12 : ************
III.6 Too much time in class was spent using clickers.
1. Strongly disagree 10 : **********
2. Disagree 23 : *********************** [2.1 +/- 1.6]
3. Neutral 9 : *********
4. Agree 2 : **
5. Strongly agree 0 :
III.7 Too many clicker questions were asked.
1. Strongly disagree 8 : ********
2. Disagree 23 : *********************** [2.1 +/- 1.4]
3. Neutral 11 : ***********
4. Agree 1 : *
5. Strongly agree 0 :
III.8 Using clickers was difficult.
1. Strongly disagree 16 : ****************
2. Disagree 22 : ********************** [1.8 +/- 2.5]
3. Neutral 3 : ***
4. Agree 1 : *
5. Strongly agree 1 : *
IV. (Optional.) Please type in any comments you may have regarding
the use of clickers in Astronomy 210.
"I think the clickers are a cool idea, and very inventive. I had never heard of them before in real classes, and i like the college exclusive idea."
"I like the use of clickers in class and the group activities in class. I sometimes feel like am way in over my head in astronomy."
"Clickers are new to me, and that may be why I enjoy them so much. But I do like the fact that I can participate and see how I do compared to the rest of the class."
"The concept of using the clickers opens up a whole new approach to getting instant answers from the students to see how we're picking it up.Can this concept be used in other situations? I also think that if the system wants to experiment with this concept, the added cost of the clickers should be absorbed.I don't enough about them to really add more insight."
"I think it's a very organized way to gauge the students' grasps of concepts."
"I feel they let us know how we're doing. How well we understand the material of the day."
"i think the clickers are a good way of interacting with the people around and the clicker questions help me learn and better understand some of the concepts learned in class"
"I think that the questions in this survey are sell suited to an Astronomy class. If I were in English I would not like to use clickers. I think that the visual models really help to understand since the actual objects are very large and impossible to observe well from multiple perspectives/distances."
"Using the clickers in class is one of my favorite activities. It helps me learn what I don't know or I can help others with what I already know. I also like seeing the percentages of people who said different answers. It is an overall great learning experience!"
"I think that the clickers are a very interactive way for us, the students, to better understand the material. Its more visual and its helpful to see what others think the answer was and why the answer wasnt right. I believe the clickers to be very helpful."
"I enjoy using the clickers! I have not had any class use clickers before and i believe they are a postive tool to further learning in the classroom."
"At first it was hard to figure out how to get how the clickers worked, but as soon as i got it working and figured out it has been kind of fun and very helpful. It worries that me sometimes that my clicker doesn't always work and that i won't get credit."
"i like using clickers and talking to other students to find out why they chose the answer that they did. it helps me understand the question better. however, i sometimes get frustrated because my clicker's signal isn't strong enough, so im not always sure that my answer gets inputed and counted for."
"It was hard to get them a; up and running. i dont like how they were cost so much money and it is sometimes hard to get my clicker to connect with the devise that picks up signals!"
"Everything was good but should remind students to make sure that the students look up their number before going to class"
"I find clickers very useful for learning. It is very helpful because it causes inter-action and helps to keep me involved in the material. I especially like discussing the clicker questions with other classmates after the initial answer has been given."
"Once i got my clicker working and knew my number, it is a nice resource."
"I think they are a great way to engage the class but I sometimes take too long to answer. And it seems that a lot of people guess on them. But I think they are fun."
"Clickers are okay but I seem to have difficulty in knowing if it is registering correctly."
"The clickers are a cool, interactive way of learning."
"I like using clickers because they allow me to solve questions by myself. After that, I can discuss the results with other people. This system helps me to understand lectures more. Finally, I can get correct answers more confidently. I strongly recommend this system."
"To a degree, the clickers simulate test, and quiz taking experiences. As a result, this should hopefully boost the confidence of the class during exams, potentially generating higher grades all around. Also, the interaction between classmates during clicker questions creates a better understanding of the material for exam days. I think all clicker questions should have two answering periods, the initial response, and the recalculated response, in order to continue interaction and comprehension."
Labels:
clickers,
education research,
SALG,
think-pair-share
20080915
Education research: preliminary feedback on clickers (Cuesta College, Physics 205A, Fall Semester 2008)
Cuesta College students taking Physics 205A (college physics, algebra-based, mandatory adjunct laboratory) at Cuesta College, San Luis Obispo, CA use numerical keypad clickers (Classroom Performance System, einstruction.com) to enter homework and to engage in peer-interaction ("think-(pair)-share") discussion questions during lecture.
During the third week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
During the third week of instruction, students were given the opportunity to evaluate the instructional components of the course, and the use of clickers in an online "Learning Resource Survey" hosted by SurveyMonkey.com. Questions from section II are adapted from the Student Assessment of Learning Gains (SALG) survey (developed by Elaine Seymour, Wisconsin Center for Education Research, University of Wisconsin-Madison), and questions from section III (III.1, III.3, III.5, and III.7) were adapted from a "Clicker Attitude Survey" (N. W. Reay, Lei Bao, and Pengfei Li, Physics Education Research Group, Ohio State University).
These are the complete survey results. Analysis will be forthcoming after more data has been compiled from future semesters. Values for the mean and standard deviations are given next to the modal response category for each question. Note that the order of questions within sections II and III were randomly scrambled for each student.
Learning Resource SurveyThe following are all of the student responses to this question, verbatim and unedited.
Cuesta College
Physics 205A Fall Semester 2008 sections 70854, 70855
(N = 45)
I. In order to receive credit for completing this survey,
first enter your first and last name below:
____
II. How much did each of the following aspects of the class help
your learning?
II.1 Lecture by instructor.
1. Strongly disagree 0 :
2. Disagree 7 : *****
3. Neutral 5 : *****
4. Agree 20 : ******************** [3.8 +/- 1.0]
5. Strongly agree 13 : *************
II.2 Doing assigned homework, to be entered using clickers.
1. Strongly disagree 1 : *
2. Disagree 1 : *
3. Neutral 7 : ******
4. Agree 23 : ********************** [4.0 +/- 0.9]
5. Strongly agree 13 : *************
II.3 Doing practice homework.
1. Strongly disagree 0 :
2. Disagree 2 : **
3. Neutral 7 : *******
4. Agree 19 : ******************* [4.1 +/- 0.8]
5. Strongly agree 17 : *****************
II.4 Using clickers to participate in class.
1. Strongly disagree 1 : *
2. Disagree 2 : **
3. Neutral 5 : *****
4. Agree 17 : ***************** [4.2 +/- 0.9]
5. Strongly agree 20 : ********************
II.5 Reading the textbook.
1. Strongly disagree 3 : ***
2. Disagree 6 : ******
3. Neutral 8 : ********
4. Agree 19 : ******************* [3.6 +/- 1.2]
5. Strongly agree 9 : *********
II.6 Demonstrations/videos in class.
1. Strongly disagree 1 : *
2. Disagree 3 : ***
3. Neutral 13 : *************
4. Agree 17 : ***************** [3.8 +/- 1.0]
5. Strongly agree 11 : ***********
II.7 Interacting with other students during class.
1. Strongly disagree 1 : *
2. Disagree 2 : **
3. Neutral 11 : ***********
4. Agree 16 : **************** [3.9 +/- 1.0]
5. Strongly agree 15 : ***************
II.8 Interacting with other students outside of class.
1. Strongly disagree 1 :
2. Disagree 6 : ******
3. Neutral 17 : *****************
4. Agree 12 : ************ [3.5 +/- 1.0]
5. Strongly agree 9 : *********
III. Answer the following statements which may or may not describe
your beliefs about the use of clickers in this class.
III.1 I like using clickers.
1. Strongly disagree 1 : *
2. Disagree 1 : *
3. Neutral 8 : ********
4. Agree 24 : ************************ [4.0 +/- 0.8]
5. Strongly agree 11 : ***********
III.2 Clickers helped me understand lectures better.
1. Strongly disagree 1 : *
2. Disagree 8 : ********
3. Neutral 9 : *********
4. Agree 20 : ******************** [3.5 +/- 1.0]
5. Strongly agree 7 : *******
III.3 I would recommend using clickers in future semesters of Physics 205A.
1. Strongly disagree 1 : *
2. Disagree 1 : *
3. Neutral 9 : *********
4. Agree 19 : ******************* [4.0 +/- 0.9]
5. Strongly agree 15 : ***************
III.4 I will avoid other classes using clickers in future semesters.
1. Strongly disagree 17 : *****************
2. Disagree 22 : ********************** [1.8 +/- 2.6]
3. Neutral 5 : *****
4. Agree 1 : *
5. Strongly agree 0 :
III.5 Clickers were a positive experience.
1. Strongly disagree 1 : *
2. Disagree 1 : *
3. Neutral 5 : *****
4. Agree 25 : ************************* [4.1 +/- 0.8]
5. Strongly agree 13 : *************
III.6 Too much time in class was spent using clickers.
1. Strongly disagree 11 : ***********
2. Disagree 20 : ******************** [2.2 +/- 1.9]
3. Neutral 9 : *********
4. Agree 3 : ***
5. Strongly agree 2 : **
III.7 Too many clicker questions were asked.
1. Strongly disagree 11 : ***********
2. Disagree 24 : ************************ [2.1 +/- 1.8]
3. Neutral 4 : ****
4. Agree 5 : *****
5. Strongly agree 0 :
III.8 Clickers should be used to collect assigned homework.
1. Strongly disagree 2 : **
2. Disagree 5 : *****
3. Neutral 10 : **********
4. Agree 21 : ********************* [3.5 +/- 1.0]
5. Strongly agree 6 : ******
III.9 Using clickers was difficult.
1. Strongly disagree 29 : ***************************** [1.4 +/- 4.3]
2. Disagree 13 : *************
3. Neutral 2 : **
4. Agree 1 : *
5. Strongly agree 0 :
IV. (Optional.) Please type in any comments you may have regarding
the use of clickers in Physics 205A.
"I believe the clickers are a very good way to teach in a classroom, i like the active learning it portrays. I do think we sometimes spend a little too much time messing with the clickers and i feel sometimes i am guessing more then i am learning. THe aspect of talking to fellow neighbors and getting their opinion really helps. Physics could possibly be a very boring class but with the clickers and the active learning it keeps me wide awake and very involved with the class, i have nothing but good words for the clickers and the way they are used in our classroom."
"I like using the clickers; it made the class more interactive and is giving me a better grasp of the subject material."
"I'm not too crazy about having to spend money on the clicker and its registration, however it is an efficient and paperless means of submitting answers to problems done both in class and for homework."
"At first I was skeptical about the use of clickers but am now seeing their usefulness. It speeds up the flow of a lecture hall-style class and allows all of us to try the questions and give an answer. In a lot of classes similar to this, the instructor works out the entire problem and then you go home and try to apply the lessons learned from watching him. With clickers, we not only can get this, but we can get immediate feedback on our strategies because we can try to apply the lessons during the actual lecture. The initial day using clickers was a little interesting because I did not know how to really use one, but they are fairly easy to master in a short space of time."
"Use of clickers is helpful in SOME situations. For example, registering attendance and correcting preassigned homework problems. But it should not be a substitute for learning through lectures. There is still tremendous value in introducing new concepts through the instructor working example problems in class. There is no substitute for witnessing the thought process of an experienced instructor during lecture. I would encourage lessened use of clickers and more lecture time for this reason. Thanks for the opportunity to opine."
"A problem I find while using the clickers is that I usually have all of the homework problems done correctly, but in the past I've had errors sending in the homework (for example, accidentally sending in the right answer to problem a when you ask for problem b). However, it may just be that the clickers take getting used to. I really like when you use clickers to see how the class is doing, but it gets stressful when it's a matter of my grade on the homework."
"Clickers are really good, to see if the class actually gets the material, and are able to do it."
"I like the clickers, they make class kind of fun, and help get you motivated to think about the question instead of just mindlessly copying down notes."
"I like the idea of using clickers for review, but not for explaining new material. I dislike entering homework on them. I realize it makes the teacher's job easier and allows him/her more time to help students, but I miss the teachers feedback about what I am doing wrong on the homework. I do worry about the extensive use of clickers in class. The clicker only tells you if you are right or wrong. It would be helpful to have a lecture first to show us how to do the problem rather than just showing us what we did wrong. The material is very staright forward now, But I have a feeling that it will get very complicated and with the clicker approach, it may cause even more frustration and confusion. It is required of us to read ahead and be prepared for class, but for those who do not understand what the book is trying to teach, the clickers will not help. Each lecture feels like it is more of a review rather than explaining the new material. In summary, this physics class (and teacher) are far better than the others at cuesta, I'm just a little nervous about the clicker approach."
"I believe that on occasion the answer has been unclear and that the answer should be presented more clearly for students who do not understand the material. Also the students should be able to see if they got the homework right or wrong since each clicker has a number the clickers are anonymous. This will help the students understand what they need to study."
"i enjoy the disscusion after we have entered our answers. it makes you fight for what you think, making you think about it more and justifying your answer."
"Your system of clicker usage punctuated by brief discussions builds confidence for "real world" situations by creating the ideal environment for expression of ideas and problem solving among individuals rather than the alternative, a one-sided and (in my opinion,) less effective presentation. thanks :)"
"Clickers are an effective way for the instructor to gage the class's progress throughout the semester."
"Love the interactivity of it - really drills the content into your brain."
"Clickers are fine in class it helps us find the right answer. Personally I would just like more demonstration problems in class and for them to be fully explained. I have trouble reading text and pulling information therefore I absorb most of my information from class lecture and example problems."
"I would like to have more lecture during the class, and less clicker questions. I feel like I leave class with no notes because we are just answering questions the whole time. More paper notes and less questions would be good. thanks"
"Clickers are a great tool, but are too heavily focused upon. Lecture isn't lecture as much as it is "Let's see if you got it right," leaving students to depend on their own reading and learning skills to learn Physics, which is a subject that needs to allow for error. I mean, if we can't even get HW wrong if we want points, it is easy to drown in the subject matter if one doesn't understand. Understanding is not advanced by the use of clickers."
"I don't like using the clickers for homework, even if you get the answer right in ur homework. Sometimes the way the clicker questions are phrased can mess up it answer"
"Huzzah for clickers, keep my attention when reviewing things I find tedious! They really worked in that area and being one of those people that doesnt like to work on things I know or "think" I know, they more then likely saved me a few points across the board already"
"i think they are a good tool for helping the instructor know what needs extra explaining"
"I really do like the concept of using clickers to encourage class participation, yet it seems to take away from the lecture portion. The lecture sems more like an internet class in which one would learn on their own through reading the book, and I believe a Physics class needs more personal instruction."
"Clickers are a waste of money and time. If the class had 200+ people I could see a reason for them but there aren't enough people in this class to warrant their use. On top of this using clickers and discussing things with classmates doesn't actually help me learn anything. I feel like I have to teach myself by reading the textbook which doesn't work for me."
"I think that you don't always give enough time in class for the clickers. I also think that there needs to be more teaching in class instead of review. I learn better when I am tought a concept and then I go home and read about it and really learn it. I think we just brush over lots of things that should really be tought to us more. If you asked questions like this in class that were clicker questions to other than just (H)i dont know how to answer this. That checked how much of an understanding we actually have."
"I think it's constructive. plus i feel like a futuristic student using it. technology is awesome."
Labels:
clickers,
education research,
SALG,
think-pair-share
20080914
Physics quiz question: stalled rocket
Physics 205A Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.40
[3.0 points.] Consider a small rocket that is launched from the ground, initially at rest at t = 0 s. After 8.0 s have elapsed, it is 610 m above the ground and is moving upwards (the +y direction) at a speed of 18.0 m/s. Assume that the rocket moves up in a straight line, and neglect air resistance. If the rocket engine shuts off at t = 8.0 s (when it is 610 m above the ground, and is moving upwards at a speed of 18.0 m/s) and undergoes free fall, what velocity does it strike the ground?
(A) –111 m/s.
(B) –109 m/s.
(C) –96 m/s.
(D) –60 m/s.
Correct answer: (A)
Since the time that the rocket will strike the ground is not given, the final velocity v_f,y can be found from the initial velocity v_i,y and the displacement delta(x) (the straight-line vector that points from the initial position to the final position, in this case -610 m):
(v_f,y)^2 - (v_i,y)^2 = 2*a_y*delta(x),
v_f,y = (+/-)sqrt((v_i,y)^2 + 2*a_y*delta(x)),
where the negative root is selected, as the rocket is moving down towards the ground as it strike it.
Response (B) is the velocity of the rocket if it had no initial velocity at 610 m above the ground; responses (C) and (D) solve for the final velocity using v_f,y = v_i,y + a_y*delta(t), assuming that the rocket takes another 8.0 s to strike the ground, with +/- sign error permutations.
Student responses
Sections 70854, 70855
(A) : 22 students
(B) : 13 students
(C) : 8 student
(D) : 4 students
"Difficulty level": 46%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.80
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.40
[3.0 points.] Consider a small rocket that is launched from the ground, initially at rest at t = 0 s. After 8.0 s have elapsed, it is 610 m above the ground and is moving upwards (the +y direction) at a speed of 18.0 m/s. Assume that the rocket moves up in a straight line, and neglect air resistance. If the rocket engine shuts off at t = 8.0 s (when it is 610 m above the ground, and is moving upwards at a speed of 18.0 m/s) and undergoes free fall, what velocity does it strike the ground?
(A) –111 m/s.
(B) –109 m/s.
(C) –96 m/s.
(D) –60 m/s.
Correct answer: (A)
Since the time that the rocket will strike the ground is not given, the final velocity v_f,y can be found from the initial velocity v_i,y and the displacement delta(x) (the straight-line vector that points from the initial position to the final position, in this case -610 m):
(v_f,y)^2 - (v_i,y)^2 = 2*a_y*delta(x),
v_f,y = (+/-)sqrt((v_i,y)^2 + 2*a_y*delta(x)),
where the negative root is selected, as the rocket is moving down towards the ground as it strike it.
Response (B) is the velocity of the rocket if it had no initial velocity at 610 m above the ground; responses (C) and (D) solve for the final velocity using v_f,y = v_i,y + a_y*delta(t), assuming that the rocket takes another 8.0 s to strike the ground, with +/- sign error permutations.
Student responses
Sections 70854, 70855
(A) : 22 students
(B) : 13 students
(C) : 8 student
(D) : 4 students
"Difficulty level": 46%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.80
20080913
Physics quiz question: displacement from a v_x(t) graph
Physics 205A Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.40
 [3.0 points.] Consider the v_x(t) graph of an object moving along a straight line, as shown at right. How far did the object move between t = 3.0 s to t = 6.0 s?
[3.0 points.] Consider the v_x(t) graph of an object moving along a straight line, as shown at right. How far did the object move between t = 3.0 s to t = 6.0 s?
(A) 1.5 m.
(B) 7.5 m.
(C) 13.5 m.
(D) 21.0 m.
Correct answer: (C)
Displacement is the area bounded by the v_x(t) graph in the time interval, which is the area of a triangle (7.5 m) and the area of a rectangle (6.0 m) added together, giving a displacement of 13.5 m. Response (A) is the difference of the triangle and rectangle areas; response (B) is the area of only the triangle; while response (D) is the twice the triangle area added to the rectangle area.
Student responses
Sections 70854, 70855
(A) : 0 students
(B) : 15 students
(C) : 29 student
(D) : 3 students
"Difficulty level": 61%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.08
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.40
 [3.0 points.] Consider the v_x(t) graph of an object moving along a straight line, as shown at right. How far did the object move between t = 3.0 s to t = 6.0 s?
[3.0 points.] Consider the v_x(t) graph of an object moving along a straight line, as shown at right. How far did the object move between t = 3.0 s to t = 6.0 s? (A) 1.5 m.
(B) 7.5 m.
(C) 13.5 m.
(D) 21.0 m.
Correct answer: (C)
Displacement is the area bounded by the v_x(t) graph in the time interval, which is the area of a triangle (7.5 m) and the area of a rectangle (6.0 m) added together, giving a displacement of 13.5 m. Response (A) is the difference of the triangle and rectangle areas; response (B) is the area of only the triangle; while response (D) is the twice the triangle area added to the rectangle area.
Student responses
Sections 70854, 70855
(A) : 0 students
(B) : 15 students
(C) : 29 student
(D) : 3 students
"Difficulty level": 61%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.08
Physics quiz question: displacement vector
Physics 205A Quiz 2, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.8
[Version 1]
[3.0 points.] An object is initially located at x = –3.40 m, and then moves to a final location at x = +0.55 m. The displacement of this object is:
(A) –3.95 m.
(B) –2.85 m.
(C) +2.85 m.
(D) +3.95 m.
Correct answer: (D)
Displacement is the final position minus the initial position:
delta(x) = x_final - x_initial = (+0.55 m) - (-3.40 m) = +3.95 m.
Response (A) is x_initial - x_final; response (B) is x_initial + x_final; while response (C) is -(x_initial + x_final).
Student responses
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 1 student
(D) : 23 students
[Version 2]
[3.0 points.] An object is initially located at x = +0.55 m, and then moves to a final location at x = –3.40 m. The displacement of this object is:
(A) –3.95 m.
(B) –2.85 m.
(C) +2.85 m.
(D) +3.95 m.
Correct answer: (A)
Displacement is the final position minus the initial position:
delta(x) = x_final - x_initial = (-3.40 m) - (+0.55 m) = -3.95 m.
Response (D) is x_initial - x_final; response (B) is x_initial + x_final; while response (C) is -(x_initial + x_final).
Student responses
Sections 70854, 70855
(A) : 13 students
(B) : 3 students
(C) : 0 students
(D) : 7 students
"Difficulty level": 76%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.39
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.8
[Version 1]
[3.0 points.] An object is initially located at x = –3.40 m, and then moves to a final location at x = +0.55 m. The displacement of this object is:
(A) –3.95 m.
(B) –2.85 m.
(C) +2.85 m.
(D) +3.95 m.
Correct answer: (D)
Displacement is the final position minus the initial position:
delta(x) = x_final - x_initial = (+0.55 m) - (-3.40 m) = +3.95 m.
Response (A) is x_initial - x_final; response (B) is x_initial + x_final; while response (C) is -(x_initial + x_final).
Student responses
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 1 student
(D) : 23 students
[Version 2]
[3.0 points.] An object is initially located at x = +0.55 m, and then moves to a final location at x = –3.40 m. The displacement of this object is:
(A) –3.95 m.
(B) –2.85 m.
(C) +2.85 m.
(D) +3.95 m.
Correct answer: (A)
Displacement is the final position minus the initial position:
delta(x) = x_final - x_initial = (-3.40 m) - (+0.55 m) = -3.95 m.
Response (D) is x_initial - x_final; response (B) is x_initial + x_final; while response (C) is -(x_initial + x_final).
Student responses
Sections 70854, 70855
(A) : 13 students
(B) : 3 students
(C) : 0 students
(D) : 7 students
"Difficulty level": 76%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.39
20080912
Astronomy clicker question: light-gathering power
Astronomy 210, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle:
An optical refractor telescope, and an optical Schmidt-Cassegrain reflector telescope, both have tubes 15 cm in diameter and 1.5 m in length, and use identical eyepieces. Which telescope has the greater light-gathering power?
(A) The refractor.
(B) The reflector.
(C) (There is a tie.)
(D) (More information is needed to determine this.)
(E) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 6 students
(B) : 6 students
(C) : 9 students
(D) : 1 student
(E) : 0 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 10 students
(B) : 2 students
(C) : 16 students
(D) : 0 students
(E) : 0 students
(F) : 1 student
Correct answer: (C) or (A)?
Both telescopes have the same diameter, and thus the same area when calculated from pi*(diameter/2)^2. However, the reflector will have a secondary mirror that will block some of the area that will receive incoming light, and so it will have slightly less LGP than the refractor.
Pre- to post- peer-interaction gains:
pre-interaction correct = 27% (A) + 41% (C)
post-interaction correct = 34% (A) + 55% (C)
Hake (normalized) gain <g> = 67% (with both (A) and (C) considered "correct" choices)
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle:
An optical refractor telescope, and an optical Schmidt-Cassegrain reflector telescope, both have tubes 15 cm in diameter and 1.5 m in length, and use identical eyepieces. Which telescope has the greater light-gathering power?
(A) The refractor.
(B) The reflector.
(C) (There is a tie.)
(D) (More information is needed to determine this.)
(E) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 6 students
(B) : 6 students
(C) : 9 students
(D) : 1 student
(E) : 0 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 10 students
(B) : 2 students
(C) : 16 students
(D) : 0 students
(E) : 0 students
(F) : 1 student
Correct answer: (C) or (A)?
Both telescopes have the same diameter, and thus the same area when calculated from pi*(diameter/2)^2. However, the reflector will have a secondary mirror that will block some of the area that will receive incoming light, and so it will have slightly less LGP than the refractor.
Pre- to post- peer-interaction gains:
pre-interaction correct = 27% (A) + 41% (C)
post-interaction correct = 34% (A) + 55% (C)
Hake (normalized) gain <g> = 67% (with both (A) and (C) considered "correct" choices)
20080911
Physics clicker question: no-drag projectile motion
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Figure 3.17
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle.
 In general, which of the following quantities is zero, for a projectile with negligible air resistance?
In general, which of the following quantities is zero, for a projectile with negligible air resistance?
(A) v_x.
(B) v_y.
(C) a_x.
(D) a_y.
(E) (More than one of the above choices.)
(F) (None of the above choices.)
(G) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 6 students
(B) : 3 students
(C) : 14 students
(D) : 3 students
(E) : 7 students
(F) : 3 students
(G) : 8 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 4 students
(B) : 2 students
(C) : 27 students
(D) : 0 students
(E) : 5 students
(F) : 4 students
(G) : 3 students
Correct answer: (C)
Under these ideal conditions, the horizontal component of velocity will be constant, and thus the horizontal component of acceleration will be zero. Realistically, with air resistance, (F) would be the most correct response.
Pre- to post- peer-interaction gains:
pre-interaction correct = 32%
post-interaction correct = 60%
Hake, or normalized gain <g> = 41%
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Figure 3.17
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the start of their learning cycle.
 In general, which of the following quantities is zero, for a projectile with negligible air resistance?
In general, which of the following quantities is zero, for a projectile with negligible air resistance?(A) v_x.
(B) v_y.
(C) a_x.
(D) a_y.
(E) (More than one of the above choices.)
(F) (None of the above choices.)
(G) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 6 students
(B) : 3 students
(C) : 14 students
(D) : 3 students
(E) : 7 students
(F) : 3 students
(G) : 8 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 4 students
(B) : 2 students
(C) : 27 students
(D) : 0 students
(E) : 5 students
(F) : 4 students
(G) : 3 students
Correct answer: (C)
Under these ideal conditions, the horizontal component of velocity will be constant, and thus the horizontal component of acceleration will be zero. Realistically, with air resistance, (F) would be the most correct response.
Pre- to post- peer-interaction gains:
pre-interaction correct = 32%
post-interaction correct = 60%
Hake, or normalized gain <g> = 41%
20080910
Astronomy clicker question: Mars finding
Astronomy 210, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle:
Consider Mars and the Earth in their orbits as shown below. (This drawing is not to scale, and orbits have been simplified as circles instead of ellipses.)

The position of Mars in the San Luis Obispo, CA sky is:
(A) near the east horizon, at sunset.
(B) near the west horizon, at sunset.
(C) near the east horizon, at sunrise.
(D) near the west horizon, at sunrise.
(E) (None of the above choices, as Mars would not be visible anywhere in the San Luis Obispo, CA sky at sunset nor sunrise.)
(F) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 12 students
(B) : 6 students
(C) : 2 students
(D) : 10 students
(E) : 0 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 27 students
(B) : 1 student
(C) : 1 student
(D) : 0 students
(E) : 0 students
(F) : 0 students
Correct answer: (A)
Mars is not visible at sunrise. However, it is visible at sunset, rising from the east horizon as the Sun sets in the west.
Pre- to post- peer-interaction gains:
pre-interaction correct = 40%
post-interaction correct = 93%
Hake (normalized) gain <g> = 89%
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the end of their learning cycle:
Consider Mars and the Earth in their orbits as shown below. (This drawing is not to scale, and orbits have been simplified as circles instead of ellipses.)

The position of Mars in the San Luis Obispo, CA sky is:
(A) near the east horizon, at sunset.
(B) near the west horizon, at sunset.
(C) near the east horizon, at sunrise.
(D) near the west horizon, at sunrise.
(E) (None of the above choices, as Mars would not be visible anywhere in the San Luis Obispo, CA sky at sunset nor sunrise.)
(F) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 12 students
(B) : 6 students
(C) : 2 students
(D) : 10 students
(E) : 0 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 27 students
(B) : 1 student
(C) : 1 student
(D) : 0 students
(E) : 0 students
(F) : 0 students
Correct answer: (A)
Mars is not visible at sunrise. However, it is visible at sunset, rising from the east horizon as the Sun sets in the west.
Pre- to post- peer-interaction gains:
pre-interaction correct = 40%
post-interaction correct = 93%
Hake (normalized) gain <g> = 89%
20080909
Physics clicker question: acceleration at top of free fall trajectory
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Multiple-Choice Question 2.1 (extended)
Students were asked the following clicker question (Classroom Performance System, einstruction.com) near the end of their learning cycle.
A ball is thrown and released such that it initially travels upwards. While it is momentarily at its highest point, its acceleration is __________. (Up = +y direction; neglect air resistance ("free fall").)
(A) +9.80 m/s^2.
(B) 0 m/s^2.
(C) –9.80 m/s^2.
(D) (More than one of the above choices.)
(E) (None of the above choices.)
(F) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 1 student
(B) : 32 students
(C) : 7 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
A separate, but related question was asked after displaying the tallied results shown above.
Which graph represents a ball thrown upwards, to falling back downwards? (Up = +y direction; neglect air resistance ("free fall"); t = 0 is immediately just after ball is released; axes are not to scale.)

Sections 70854, 70855
(A) : 7 students
(B) : 24 students
(C) : 2 students
(D) : 0 students
(E) : 0 students
(F) : 1 student
(G) : 5 students
(H) : 2 students
Correct answer: (B)
Whole-class discussion facilitated by the instructor goes over the types of free fall motion the other graphs (A), (C) and (D) represent, but the key to understanding graph (B) is that the upwards velocity decreases (becomes a smaller positive number) until it is momentarily zero at its highest position, and then this velocity increases downwards (becomes a larger negative number) as the ball falls back downwards.
The original question ("A ball is thrown and released such that it initially travels upwards") was asked again, with the following results.
Sections 70854, 70855
(A) : 0 students
(B) : 7 students
(C) : 34 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
In this whole-class discussion, students realize that the slope of the v_y versus t graph gives the acceleration, which is always a constant negative value, even when the velocity is momentarily zero, and thus a_y = -9.8 m/s^2 is the acceleration throughout the trajectory of the ball.
A student asked when the speed of the ball "matters" (i.e., when does drag become important?). Not in free fall (zero air resistance) conditions, but it does matter under realistic conditions, especially with greater and greater speeds.
Pre- to post- peer-interaction gains:
pre-interaction correct = 18%
post-interaction correct = 83%
Hake, or normalized gain <g> = 79%
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Multiple-Choice Question 2.1 (extended)
Students were asked the following clicker question (Classroom Performance System, einstruction.com) near the end of their learning cycle.
A ball is thrown and released such that it initially travels upwards. While it is momentarily at its highest point, its acceleration is __________. (Up = +y direction; neglect air resistance ("free fall").)
(A) +9.80 m/s^2.
(B) 0 m/s^2.
(C) –9.80 m/s^2.
(D) (More than one of the above choices.)
(E) (None of the above choices.)
(F) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 1 student
(B) : 32 students
(C) : 7 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
A separate, but related question was asked after displaying the tallied results shown above.
Which graph represents a ball thrown upwards, to falling back downwards? (Up = +y direction; neglect air resistance ("free fall"); t = 0 is immediately just after ball is released; axes are not to scale.)

Sections 70854, 70855
(A) : 7 students
(B) : 24 students
(C) : 2 students
(D) : 0 students
(E) : 0 students
(F) : 1 student
(G) : 5 students
(H) : 2 students
Correct answer: (B)
Whole-class discussion facilitated by the instructor goes over the types of free fall motion the other graphs (A), (C) and (D) represent, but the key to understanding graph (B) is that the upwards velocity decreases (becomes a smaller positive number) until it is momentarily zero at its highest position, and then this velocity increases downwards (becomes a larger negative number) as the ball falls back downwards.
The original question ("A ball is thrown and released such that it initially travels upwards") was asked again, with the following results.
Sections 70854, 70855
(A) : 0 students
(B) : 7 students
(C) : 34 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
In this whole-class discussion, students realize that the slope of the v_y versus t graph gives the acceleration, which is always a constant negative value, even when the velocity is momentarily zero, and thus a_y = -9.8 m/s^2 is the acceleration throughout the trajectory of the ball.
A student asked when the speed of the ball "matters" (i.e., when does drag become important?). Not in free fall (zero air resistance) conditions, but it does matter under realistic conditions, especially with greater and greater speeds.
Pre- to post- peer-interaction gains:
pre-interaction correct = 18%
post-interaction correct = 83%
Hake, or normalized gain <g> = 79%
20080908
Astronomy quiz question: northwest setting Sun
Astronomy 210 Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] Which month would the Sun set in the northwest horizon, as seen by an observer in San Luis Obispo, CA?
(A) March or September.
(B) June.
(C) December.
(D) (None of the above choices, as it is not possible for the sun to set in the northwest horizon in San Luis Obispo, CA.)
Correct answer: (B)
In June (summer solstice), the Sun will rise northeast, pass the meridian very close to the zenith, and then set northwest. In March or September (vernal/autumnal equinoxes), the Sun will rise directly from the east and set in the west, while in December (winter solstice) the Sun will rise in the southeast, pass the meridian closer down towards the horizon, and eventually set southwest.
Student responses
Section 70158
(A) : 24 students
(B) : 27 students
(C) : 17 students
(D) : 7 students
"Difficulty level": 39%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.43
Cuesta College, San Luis Obispo, CA
[4.0 points.] Which month would the Sun set in the northwest horizon, as seen by an observer in San Luis Obispo, CA?
(A) March or September.
(B) June.
(C) December.
(D) (None of the above choices, as it is not possible for the sun to set in the northwest horizon in San Luis Obispo, CA.)
Correct answer: (B)
In June (summer solstice), the Sun will rise northeast, pass the meridian very close to the zenith, and then set northwest. In March or September (vernal/autumnal equinoxes), the Sun will rise directly from the east and set in the west, while in December (winter solstice) the Sun will rise in the southeast, pass the meridian closer down towards the horizon, and eventually set southwest.
Student responses
Section 70158
(A) : 24 students
(B) : 27 students
(C) : 17 students
(D) : 7 students
"Difficulty level": 39%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.43
20080907
Astronomy quiz question: zenith star set
Astronomy 210 Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] An observer in San Luis Obispo, CA observes a constellation located at the zenith. This constellation will:
(A) never set below the horizon, as it is a circumpolar constellation.
(B) eventually set somewhere near the southwest horizon.
(C) eventually set somewhere near the northwest horizon.
(D) (None of the above choices, as it is not possible for a constellation to be at the zenith in San Luis Obispo, CA.)
Correct answer: (C)
Using a starwheel, selecting any constellation (e.g., Lyra) that is at the zenith at its highest position, will eventually set on the northwest horizon. (For Lyra, it is at the zenith as it passes the meridian at 8:00 PM on August 25, and will set at 5:00 AM the next day.) Or from discussion on paths of the sun, objects that rise northeast will pass the meridian closer to the zenith, and set northwest, than objects that rise in the southeast, which will pass the meridian closer to the horizon, and eventually set southwest.
Some students may be confusing the hub of the starwheel (corresponding to the celestial north pole, near which Polaris lies) with the zenith (corresponding to the geometric center of the blue oval representing the visible portion of the celestial sphere above the horizon).
Student responses
Section 70158
(A) : 38 students
(B) : 10 students
(C) : 21 students
(D) : 6 students
"Difficulty level": 34%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.43
Cuesta College, San Luis Obispo, CA
[4.0 points.] An observer in San Luis Obispo, CA observes a constellation located at the zenith. This constellation will:
(A) never set below the horizon, as it is a circumpolar constellation.
(B) eventually set somewhere near the southwest horizon.
(C) eventually set somewhere near the northwest horizon.
(D) (None of the above choices, as it is not possible for a constellation to be at the zenith in San Luis Obispo, CA.)
Correct answer: (C)
Using a starwheel, selecting any constellation (e.g., Lyra) that is at the zenith at its highest position, will eventually set on the northwest horizon. (For Lyra, it is at the zenith as it passes the meridian at 8:00 PM on August 25, and will set at 5:00 AM the next day.) Or from discussion on paths of the sun, objects that rise northeast will pass the meridian closer to the zenith, and set northwest, than objects that rise in the southeast, which will pass the meridian closer to the horizon, and eventually set southwest.
Some students may be confusing the hub of the starwheel (corresponding to the celestial north pole, near which Polaris lies) with the zenith (corresponding to the geometric center of the blue oval representing the visible portion of the celestial sphere above the horizon).
Student responses
Section 70158
(A) : 38 students
(B) : 10 students
(C) : 21 students
(D) : 6 students
"Difficulty level": 34%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.43
20080906
Astronomy clicker question: transit of Mercury
Astronomy 210, fall semester 2008
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the middle of their learning cycle:
In a rare event, the planet Mercury was observed in November 2006 as a tiny dark dot in the middle of the disk of the sun, for observers in San Luis Obispo, CA. Which shadow zone were these observers in when that happened?
(A) The umbra of Mercury.
(B) The penumbra of Mercury.
(C) The negative shadow of Mercury.
(D) The umbra of Earth.
(E) The penumbra of Earth.
(F) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 7 students
(B) : 0 students
(C) : 16 students
(D) : 0 students
(E) : 2 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 1 student
(B) : 0 students
(C) : 25 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
Correct answer: (C)
The negative shadow zone is directly behind the umbra of Mercury, where from that location its angular size is too small to completely cover the sun.
Pre- to post- peer-interaction gains:
pre-interaction correct = 64%
post-interaction correct = 96%
Hake (normalized) gain <g> = 89%
Cuesta College, San Luis Obispo, CA
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the middle of their learning cycle:
In a rare event, the planet Mercury was observed in November 2006 as a tiny dark dot in the middle of the disk of the sun, for observers in San Luis Obispo, CA. Which shadow zone were these observers in when that happened?
(A) The umbra of Mercury.
(B) The penumbra of Mercury.
(C) The negative shadow of Mercury.
(D) The umbra of Earth.
(E) The penumbra of Earth.
(F) (I'm lost, and don't know how to answer this.)
Section 70160
(A) : 7 students
(B) : 0 students
(C) : 16 students
(D) : 0 students
(E) : 2 students
(F) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Section 70160
(A) : 1 student
(B) : 0 students
(C) : 25 students
(D) : 0 students
(E) : 0 students
(F) : 0 students
Correct answer: (C)
The negative shadow zone is directly behind the umbra of Mercury, where from that location its angular size is too small to completely cover the sun.
Pre- to post- peer-interaction gains:
pre-interaction correct = 64%
post-interaction correct = 96%
Hake (normalized) gain <g> = 89%
20080905
Solar system scribble
 "Warning: not to scale" by D. T.
"Warning: not to scale" by D. T.Astronomy 210L
Fall Semester 2008
Cuesta College, San Luis Obispo, CA
This doodle was found on the back of a weekly current events quiz for introductory astronomy lab. Note that Pluto is not included with the rest of the planets!
Labels:
Pluto,
solar system,
student scribble
20080904
Astronomy quiz question: Moon directly overhead
Astronomy 210 Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[Version 1]
[4.0 points.] What time is it when the waxing gibbous moon is highest overhead?
(A) 12 PM (noon).
(B) 3 PM (afternoon).
(C) 6 PM (sunset).
(D) 9 PM (evening).
(E) 12 AM (midnight).
(F) 3 AM (wee hours).
(G) 6 AM (sunrise).
(H) 9 AM (morning).
Correct answer: (D)
This is apparent once the Moon has been placed correctly in its orbit around the Earth, relative to the direction of sunlight on the Earth-Moon diagram. (Doing the "+/- 6 hour trick" results in this moon rising at (B) 3 PM, and setting at (F) 3 AM.)
Student responses
Section 70160
(A) : 0 students
(B) : 4 students
(C) : 0 students
(D) : 8 students
(E) : 0 students
(F) : 0 students
(G) : 0 students
(H) : 3 students
[Version 2]
[4.0 points.] What time is it when the waning gibbous moon is highest overhead?
(A) 12 PM (noon).
(B) 3 PM (afternoon).
(C) 6 PM (sunset).
(D) 9 PM (evening).
(E) 12 AM (midnight).
(F) 3 AM (wee hours).
(G) 6 AM (sunrise).
(H) 9 AM (morning).
Correct answer: (F)
This is apparent once the Moon has been placed correctly in its orbit around the Earth, relative to the direction of sunlight on the Earth-Moon diagram. (Doing the "+/- 6 hour trick" results in this moon rising at (D) 9 PM, and setting at (H) 9 AM.)
Student responses
Section 70160
(A) : 0 students
(B) : 2 students
(C) : 1 student
(D) : 3 students
(E) : 1 student
(F) : 8 students
(G) : 2 students
(H) : 0 students
"Difficulty level": 54%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.56
Cuesta College, San Luis Obispo, CA
[Version 1]
[4.0 points.] What time is it when the waxing gibbous moon is highest overhead?
(A) 12 PM (noon).
(B) 3 PM (afternoon).
(C) 6 PM (sunset).
(D) 9 PM (evening).
(E) 12 AM (midnight).
(F) 3 AM (wee hours).
(G) 6 AM (sunrise).
(H) 9 AM (morning).
Correct answer: (D)
This is apparent once the Moon has been placed correctly in its orbit around the Earth, relative to the direction of sunlight on the Earth-Moon diagram. (Doing the "+/- 6 hour trick" results in this moon rising at (B) 3 PM, and setting at (F) 3 AM.)
Student responses
Section 70160
(A) : 0 students
(B) : 4 students
(C) : 0 students
(D) : 8 students
(E) : 0 students
(F) : 0 students
(G) : 0 students
(H) : 3 students
[Version 2]
[4.0 points.] What time is it when the waning gibbous moon is highest overhead?
(A) 12 PM (noon).
(B) 3 PM (afternoon).
(C) 6 PM (sunset).
(D) 9 PM (evening).
(E) 12 AM (midnight).
(F) 3 AM (wee hours).
(G) 6 AM (sunrise).
(H) 9 AM (morning).
Correct answer: (F)
This is apparent once the Moon has been placed correctly in its orbit around the Earth, relative to the direction of sunlight on the Earth-Moon diagram. (Doing the "+/- 6 hour trick" results in this moon rising at (D) 9 PM, and setting at (H) 9 AM.)
Student responses
Section 70160
(A) : 0 students
(B) : 2 students
(C) : 1 student
(D) : 3 students
(E) : 1 student
(F) : 8 students
(G) : 2 students
(H) : 0 students
"Difficulty level": 54%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.56
Astronomy quiz question: starrise to starset time
Astronomy 210 Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
[4.0 points.] A star that rises from the northeast horizon in San Luis Obispo, CA will take approximately how many hours until it sets in the northwest horizon?
(A) Less than 12 hours.
(B) More than 12 hours.
(C) (It cannot be determined how many hours the star will take to set, unless the season is known.)
(D) (None of the above choices, as it is not possible for a star to rise from the northeast horizon in San Luis Obispo, CA.)
Correct answer: (B)
Using a starwheel, selecting any star (e.g., Pollux) that rises from the northeast horizon, and finding the difference in times when it is on the northeast horizon, and eventually setting on the northwest horizon on the same/consecutive day(s) will result in more than 12 hours elapsed. (For Pollux, it rises at 2:00 AM on August 25, and will set at 5:30 PM later that same day.) Or from discussion on paths of the sun, objects that rise north of east will take longer than 12 hours to rise and set, compared to objects that rise directly in the east (exactly 12 hours); or objects that rise south of east (less than 12 hours).
Student responses
Section 70160
(A) : 12 students
(B) : 10 students
(C) : 8 students
(D) : 1 student
(no response) : 1 student
"Difficulty level": 38%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.44
Cuesta College, San Luis Obispo, CA
[4.0 points.] A star that rises from the northeast horizon in San Luis Obispo, CA will take approximately how many hours until it sets in the northwest horizon?
(A) Less than 12 hours.
(B) More than 12 hours.
(C) (It cannot be determined how many hours the star will take to set, unless the season is known.)
(D) (None of the above choices, as it is not possible for a star to rise from the northeast horizon in San Luis Obispo, CA.)
Correct answer: (B)
Using a starwheel, selecting any star (e.g., Pollux) that rises from the northeast horizon, and finding the difference in times when it is on the northeast horizon, and eventually setting on the northwest horizon on the same/consecutive day(s) will result in more than 12 hours elapsed. (For Pollux, it rises at 2:00 AM on August 25, and will set at 5:30 PM later that same day.) Or from discussion on paths of the sun, objects that rise north of east will take longer than 12 hours to rise and set, compared to objects that rise directly in the east (exactly 12 hours); or objects that rise south of east (less than 12 hours).
Student responses
Section 70160
(A) : 12 students
(B) : 10 students
(C) : 8 students
(D) : 1 student
(no response) : 1 student
"Difficulty level": 38%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.44
Labels:
astronomy multiple-choice question,
stars,
starwheel,
sunrise,
sunset
Physics quiz question: dimensional analysis of pendulum period
Physics 205A Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 1.30
[Version 1]
[3.0 points.] Using dimensional analysis, how does the period T of a pendulum (measured in seconds) depend on some, or all of the following properties: m is the mass of the pendulum bob, L is the length of the pendulum string, and g is the gravitational field strength (measured in units of m/s^2)?
(A) T = L^(1/2) * g^(-1/2).
(B) T = m^(1/2) * L^(-1/2).
(C) T = g^(1/2) * m^(-1/2).
(D) T = g^(1/2) * L^(1/2) * m^(-1/2).
Correct answer: (A)
Starting with a prototype equation with arbitrary exponents p, q, and r:
T = m^(p) * L^(q) * g^(r),
then substituting in their respective units and gathering like terms (here m is for meters, and not for mass):
s = kg^(p) * m^(q) * (m/s^2)^(r);
s = kg^(p) * m^(q+r) * s^(-2*r).
By inspection, p = 0, as there are no kilogram units on the left side of the equation. Thus r = -1/2, in order to match the single unit of seconds on the left side of the equation with the units of seconds raised to the -2*r power on the right side. Thus for the sole remaining meters unit, 0 = q + r, where r = -1/2 gives q = 1/2, giving the completed result T = L^(1/2) * m^(-1/2).
Student responses
Sections 70854, 70855
(A) : 9 students
(B) : 5 students
(C) : 6 students
(D) : 6 students
[Version 2]
[3.0 points.] Using dimensional analysis, how does the period T of a pendulum (measured in seconds) depend on some, or all of the following properties: m is the mass of the pendulum bob, L is the length of the pendulum string, and g is the gravitational field strength (measured in units of m/s^2)?
(A) T = g^(1/2) * L^(1/2) * m^(-1/2).
(B) T = g^(1/2) * m^(-1/2).
(C) T = m^(1/2) * L^(-1/2).
(D) T = L^(1/2) * g^(-1/2).
Correct answer: (D)
Student responses
Sections 70854, 70855
(A) : 11 students
(B) : 3 students
(C) : 3 students
(D) : 7 students
"Difficulty level": 30%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.7
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 1.30
[Version 1]
[3.0 points.] Using dimensional analysis, how does the period T of a pendulum (measured in seconds) depend on some, or all of the following properties: m is the mass of the pendulum bob, L is the length of the pendulum string, and g is the gravitational field strength (measured in units of m/s^2)?
(A) T = L^(1/2) * g^(-1/2).
(B) T = m^(1/2) * L^(-1/2).
(C) T = g^(1/2) * m^(-1/2).
(D) T = g^(1/2) * L^(1/2) * m^(-1/2).
Correct answer: (A)
Starting with a prototype equation with arbitrary exponents p, q, and r:
T = m^(p) * L^(q) * g^(r),
then substituting in their respective units and gathering like terms (here m is for meters, and not for mass):
s = kg^(p) * m^(q) * (m/s^2)^(r);
s = kg^(p) * m^(q+r) * s^(-2*r).
By inspection, p = 0, as there are no kilogram units on the left side of the equation. Thus r = -1/2, in order to match the single unit of seconds on the left side of the equation with the units of seconds raised to the -2*r power on the right side. Thus for the sole remaining meters unit, 0 = q + r, where r = -1/2 gives q = 1/2, giving the completed result T = L^(1/2) * m^(-1/2).
Student responses
Sections 70854, 70855
(A) : 9 students
(B) : 5 students
(C) : 6 students
(D) : 6 students
[Version 2]
[3.0 points.] Using dimensional analysis, how does the period T of a pendulum (measured in seconds) depend on some, or all of the following properties: m is the mass of the pendulum bob, L is the length of the pendulum string, and g is the gravitational field strength (measured in units of m/s^2)?
(A) T = g^(1/2) * L^(1/2) * m^(-1/2).
(B) T = g^(1/2) * m^(-1/2).
(C) T = m^(1/2) * L^(-1/2).
(D) T = L^(1/2) * g^(-1/2).
Correct answer: (D)
Student responses
Sections 70854, 70855
(A) : 11 students
(B) : 3 students
(C) : 3 students
(D) : 7 students
"Difficulty level": 30%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.7
20080903
Physics quiz question: significant figures addition rule
Physics 205A Quiz 1, fall semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 1.12
[Version 1]
Evaluate the following calculation, using an appropriate number of significant figures and/or decimal places.
4.26 g + 10.0 mg = ?
(A) 4.27 g.
(B) 4.3 g.
(C) 4.36 g.
(D) 4.4 g.
Correct answer: (A)
In order to apply the addition-subtraction rule of limiting decimal places, the 10.0 mg is converted into grams such that:
4.26 g + 10.0 mg = 4.26 g + 0.0100 g = 4.27 g,
limited to two decimal places by the first term.
Student responses
Sections 70854, 70855
(A) : 15 students
(B) : 8 students
(C) : 3 students
(D) : 2 students
[Version 2]
[3.0 points.] Evaluate the following calculation, using an appropriate number of significant figures and/or decimal places.
4.26 g + 100.0 mg = ?
(A) 4.27 g.
(B) 4.3 g.
(C) 4.36 g.
(D) 4.4 g.
Correct answer: (C)
In order to apply the addition-subtraction rule of limiting decimal places, the 10.0 mg is converted into grams such that:
4.26 g + 100.0 mg = 4.26 g + 0.1000 g = 4.36 g,
again, limited to two decimal places by the first term.
Student responses
Sections 70854, 70855
(A) : 1 student
(B) : 3 students
(C) : 16 students
(D) : 5 students
"Difficulty level": 57%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.2
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 1.12
[Version 1]
Evaluate the following calculation, using an appropriate number of significant figures and/or decimal places.
4.26 g + 10.0 mg = ?
(A) 4.27 g.
(B) 4.3 g.
(C) 4.36 g.
(D) 4.4 g.
Correct answer: (A)
In order to apply the addition-subtraction rule of limiting decimal places, the 10.0 mg is converted into grams such that:
4.26 g + 10.0 mg = 4.26 g + 0.0100 g = 4.27 g,
limited to two decimal places by the first term.
Student responses
Sections 70854, 70855
(A) : 15 students
(B) : 8 students
(C) : 3 students
(D) : 2 students
[Version 2]
[3.0 points.] Evaluate the following calculation, using an appropriate number of significant figures and/or decimal places.
4.26 g + 100.0 mg = ?
(A) 4.27 g.
(B) 4.3 g.
(C) 4.36 g.
(D) 4.4 g.
Correct answer: (C)
In order to apply the addition-subtraction rule of limiting decimal places, the 10.0 mg is converted into grams such that:
4.26 g + 100.0 mg = 4.26 g + 0.1000 g = 4.36 g,
again, limited to two decimal places by the first term.
Student responses
Sections 70854, 70855
(A) : 1 student
(B) : 3 students
(C) : 16 students
(D) : 5 students
"Difficulty level": 57%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.2
20080902
Physics quiz question: ratio of sides of increased square area
Physics 205A Quiz 1, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Comprehensive Problem 1.49
[3.0 points.] The area of a square plot of land is increased by a factor of 1.5. By what factor did the side of this plot change?
(A) 1.2.
(B) 1.3.
(C) 1.5.
(D) 2.3.
Correct answer: (A)
A_new = 1.5*A_old, where A_new = s_new*s_new, and A_old = s_old*s_old. Thus:
(s_new)/(s_old) = sqrt(A_new)/sqrt(A_old) = sqrt(1.5*A_old/A_old) = sqrt(1.5),
which is 1.224744871..., or to two significant figures, 1.2.
Student responses
Sections 70854, 70855
(A) : 25 students
(B) : 3 students
(C) : 19 students
(D) : 5 students
"Difficulty level": 48%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.7
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Comprehensive Problem 1.49
[3.0 points.] The area of a square plot of land is increased by a factor of 1.5. By what factor did the side of this plot change?
(A) 1.2.
(B) 1.3.
(C) 1.5.
(D) 2.3.
Correct answer: (A)
A_new = 1.5*A_old, where A_new = s_new*s_new, and A_old = s_old*s_old. Thus:
(s_new)/(s_old) = sqrt(A_new)/sqrt(A_old) = sqrt(1.5*A_old/A_old) = sqrt(1.5),
which is 1.224744871..., or to two significant figures, 1.2.
Student responses
Sections 70854, 70855
(A) : 25 students
(B) : 3 students
(C) : 19 students
(D) : 5 students
"Difficulty level": 48%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.7
20080901
Physics clicker question: position vs. time graph fastest speed
Physics 205A, Fall Semester 2008
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.14(a) (extended)
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the beginning of their learning cycle, after learning about the "Physics chain of pain" connections between kinematics graphs.
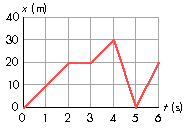 In which time interval(s) does the object have the fastest speed?
In which time interval(s) does the object have the fastest speed?
(A) t = 0 to t = 2 s.
(B) t = 2 s to t = 3 s.
(C) t = 3 s to t = 4 s.
(D) t = 4 s to t = 5 s.
(E) t = 5 s to t = 6 s.
(F) (More than one of the above choices apply.)
(G) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 7 students
(D) : 21 students
(E) : 17 students
(F) : 1 student
(G) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 0 students
(D) : 38 students
(E) : 8 students
(F) : 0 students
(G) : 0 students
Correct answer: (D)
While the time interval from t = 5 s to t = 6 s represents the fastest positive velocity, the t = 4 s to t = 5 s time interval has the steepest slope, corresponding to the fastest velocity magnitude, or speed. Parsing the statement "fastest speed" then, is "steepest |slope|."
Pre- to post- peer-interaction gains:
pre-interaction correct = 46%
post-interaction correct = 83%
Hake, or normalized gain <g> = 68%
Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 2.14(a) (extended)
Students were asked the following clicker question (Classroom Performance System, einstruction.com) at the beginning of their learning cycle, after learning about the "Physics chain of pain" connections between kinematics graphs.
 In which time interval(s) does the object have the fastest speed?
In which time interval(s) does the object have the fastest speed?(A) t = 0 to t = 2 s.
(B) t = 2 s to t = 3 s.
(C) t = 3 s to t = 4 s.
(D) t = 4 s to t = 5 s.
(E) t = 5 s to t = 6 s.
(F) (More than one of the above choices apply.)
(G) (I'm lost, and don't know how to answer this.)
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 7 students
(D) : 21 students
(E) : 17 students
(F) : 1 student
(G) : 0 students
This question was asked again after displaying the tallied results with the lack of consensus, with the following results. No comments were made by the instructor, in order to see if students were going to be able to discuss and determine the correct answer among themselves.
Sections 70854, 70855
(A) : 0 students
(B) : 0 students
(C) : 0 students
(D) : 38 students
(E) : 8 students
(F) : 0 students
(G) : 0 students
Correct answer: (D)
While the time interval from t = 5 s to t = 6 s represents the fastest positive velocity, the t = 4 s to t = 5 s time interval has the steepest slope, corresponding to the fastest velocity magnitude, or speed. Parsing the statement "fastest speed" then, is "steepest |slope|."
Pre- to post- peer-interaction gains:
pre-interaction correct = 46%
post-interaction correct = 83%
Hake, or normalized gain <g> = 68%
Subscribe to:
Posts (Atom)