
Look at all these batteries. Just look at them. While we might think of them as "containing" electrical potential energy, or even as voltage "sources," we'll see that just two charges can "contain" electric potential energy, and that just a single charge can be thought of as a voltage "source." In subsequent presentations we'll explore more complex voltage "sources" that "contain" electric potential energy:
capacitors,
batteries, and
household electric outlets.

In this presentation we will consider different approaches to analyze electric potential energy.

First, a direct approach to electric potential energy.

Recall that in the
direct approach to electric forces, a source charge
q1 can be said to exert a force
F on a separate test charge
q2.
Similarly, a direct approach to electric potential energy is that a source charge
q1 can be said to store electric potential energy
EPE on with a separate test charge charge
q2.

∆
EPE changes in this electric potential energy are caused by moving the source charge and test charge closer together, or moving them farther apart.
EPE can be increased (thus making ∆
EPE positive) by pushing together like-sign charges (positive-positive, or negative-negative), or pulling apart opposite-sign charges (positive-negative, or negative-postive). This is because it takes work to push together like-sign charges (which repel, and don't want to be pushed together); or takes work to pull apart opposite-sign charges (which attract, and don't want to be pulled apart).
On the other hand, work is done by charges that are allowed to do what they want to, thus decreasing
EPE (and making ∆
EPE negative), by letting like-sign charges (positive-positive, or negative-negative) move farther apart from each other (because these charges repel); or letting opposite-sign charges (positive-negative, or negative-positive) move closer to each other (because these charges attract).

The value of the electric potential energy of a source charge
q1 and test charge
q2 at a certain distance
r from each other can be calculated by an equation that looks similar to the magnitude of the electric force (but note the
r–1 dependence for electric potential energy, as opposed to the
r-2 dependence of electric forces). With the constant
k, units of coulombs
2 and meters cancel, leaving units of N·m, which is what we have seen
last semester as joules.
(Note that this equation calculates the value of electric potential energy
EPE of two charges at a fixed separation distance from each other. In order to find the ∆
EPE change in electric potential energy, you would need to calculate the initial
EPEi and final
EPEf electric potential energies of the two charges at their initial
ri and final
rf separation distances.)

Second, the two-step approach to electric potential energy.

Recall that in the
two-step approach to electric forces, a source charge
Q can be said to create an electric field
E everywhere around itself, and then this electric field exerts a force
F on a separate test charge
q.

Similarly, a two-step approach to electric potential energy is that a source charge
Q can be said to create a potential
V everywhere around itself, and this potential stores electric potential energy
EPE with a separate test charge charge
q.

Let's focus on the first step of this two-step model. The source charge
Q creates a potential
V everywhere around it. The magnitude of this potential can be calculated for a location at a distance
r from the source charge, and has units of joules per coulomb (J/C), which is often re-expressed as volts (V). The sign of the potential depends on the sign of the source charge
Q: if the source charge is positive, then the values of the potential everywhere around it are positive; if the source charge is negative, then the values of the potential everywhere around it are negative.
 Recall
Recall that electric fields surrounding a single source charge are visualized as lines emanating outwards from, or pointing in towards the source charge. In contrast, the potentials surrounding a single source charge are visualized (here, in two-dimensions) as circles, as every location at the same distance
r from the source charge must have the same value of potential, such that these circles are often referred to as
equipotentials.
Note that the direction of electric field lines is indicative of the relative values of the equipotentials: for the positive source charge, each subsequent outer equipotential corresponds to smaller and smaller positive values of potential (due to the
r–1 dependence); for the negative source charge, each subsequent inner potential equipotential corresponds to larger and larger negative values of potential. So in either case, electric field lines point towards
decreasing electric potential values.

A nice visualization is to imagine that a positive source charge creates a "peak" of potential around it--as you get closer in towards this positive source charge, the values of potential become bigger and bigger positive numbers, corresponding to a increase in elevation. In contrast, a negative source charge creates a "well" of potential around it--as you get closer in towards this negative source charge, the values of potential become bigger and bigger negative numbers, corresponding to a decrease in elevation.

So where does "voltage" come in? The amount of potential (which is measured in volts) at a location in space is often called the "voltage." So "potential" and "voltage" really mean the same thing (and just to confuse things even further, "electrical tension" is an equivalent archaic term). Get used to these terms, as we will be referring to them interchangeably through the remainder of this semester. Nobody ever thinks this is a big deal, so deal with it. (But yes, it is a big deal.)

Now what? If there is another charge anywhere in the presence of a potential, this potential will store electrical potential energy with the test charge
q. In this equation, the electrical potential energy
EPE stored by the test charge
q is the test charge
q multiplied by the potential
V at the test charge's location. Since the test charge
q could be positive or negative, and the potential
V could have positive or negative values, then the electrical potential energy stored would have the correct sign depending the the product of these two signs.
(Notice that coulombs (C) multiplied by volts (V, or J/C) results in units of joules (J). In this sense potential or "voltage" can be said to be "potential" potential energy, that is, a location in space will only have a value for potential (measured in volts, or joules per coulomb), but any test charge
q placed at this location in space will then have a value for electric potential energy (measured in joules) given by the product of the potential and amount of charge placed there.)
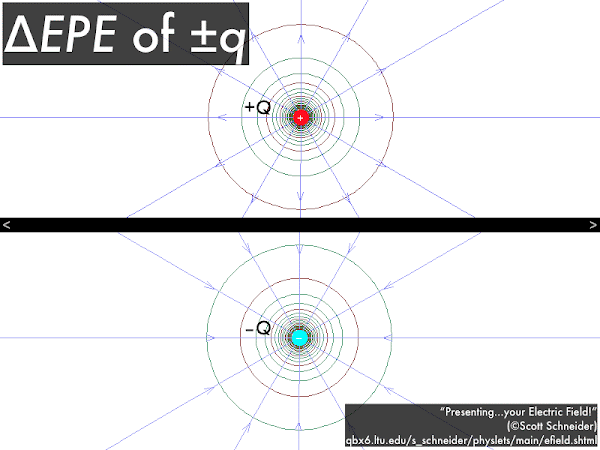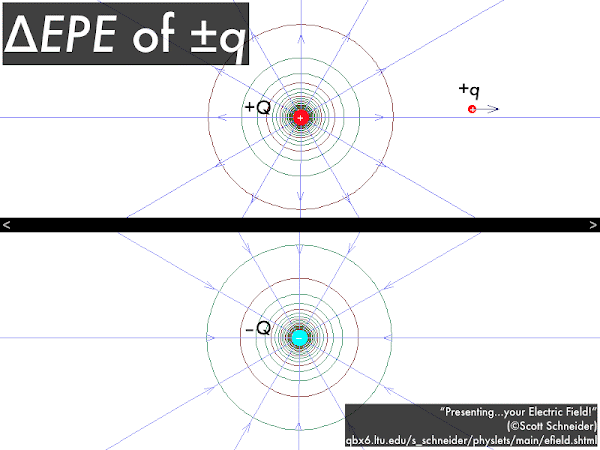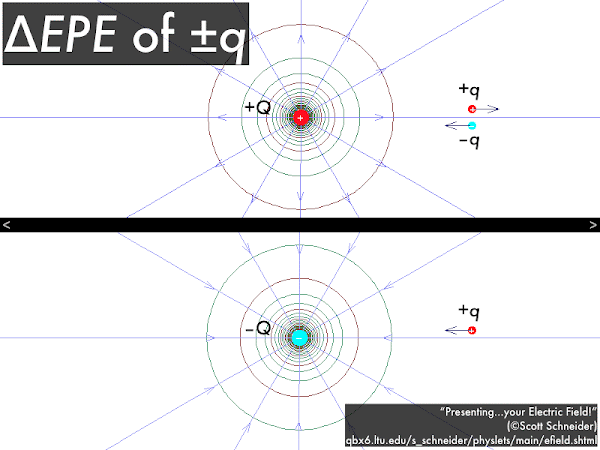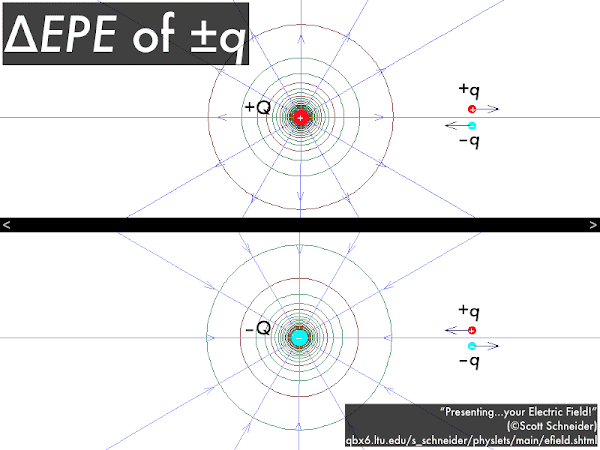
Here, from before, we show the electrical fields and potentials filling in all space surrounding a positive or a negative source charge. Putting a positive test charge in the presence of these electrical fields and potentials will cause an electrical force to be exerted along a field line,
which would also point in the direction of decreasing potential and decreasing potential energy; while putting a negative test charge in the presence of these electrical fields and potentials will cause an electrical force to be exerted in the opposite direction of a field line,
which would point in the direction of increasing potential, but decreasing potential energy.
In any case, as a check the direction of the force on any source charge
q should be attractive or repulsive depending on whether it has the opposite or same sign as the source charge
Q, and also check that the source charge
q moves in the direction that would decrease its electric potential energy. However, positive test charges move in the direction of decreasing potential, while negative test charges move in the direction of increasing potential! (If all this sounds confusing, at least be assured that these rules are consistent.)

As previously above, we visualized a positive source charge +
Q as a "peak." Here we have a positive test charge +
q as a hapless snowmobiler on this "peak." Initially as the snowmobiler rides up the "peak," increasing his potential and increasing his potential energy, work is required to push it "uphill" (provided by an external source, here the snowmobile engine). Left alone, the snowmobile and snowmobiler will slide "downhill," in the direction of decreasing potential and decreasing potential energy (as we have seen before, for two positive charges separating from each other). What would happen if the snowmobiler were a
negative test charge –
q? Then we would observe the very odd behavior of this negative snowmobiler sliding "uphill," in the direction in
increasing potential--but this would be the direction of
decreasing potential energy, as we have seen before, for a negative charge and a positive charge getting closer to each other.
What would happen if there was a negative source charge –
Q creating a "well?" Then a positive test charge +
q snowmobiler, left alone, would slide "downhill," in the direction of decreasing potential and decreasing potential energy (as we have seen before, for a negative charge and positive charge getting closer to each other). Then consider the very odd case of a
negative test charge –
q snowmobiler sliding on this "well"--we would observe the very odd behavior of this negative snowmobiler sliding "uphill," in the direction in
increasing potential--but this would be the direction of
decreasing potential energy, as we have seen before, for two negative charges separating from each other. (Video source: "
Grazy hill climb crash with go pro cam.")
















No comments:
Post a Comment