Presentation: capacitors

Look at these capacitors. Just look at them. How dangerous could these be? One of them even looks like an M&M™...

Well, maybe just a little dangerous, when embedded in protective clothing for self-protection purposes. But why? Are capacitors "shocking" because they store charge? Voltage? Energy? All three? (Video link: "No-Contact™ Conducted Energy Clothing.")

In this presentation we will look at the construction of capacitors, and how and what they "store."

First, the construction and charging of capacitors.

Even though capacitors come in many different shapes and sizes, carefully taking one apart will demonstrate certain common features. In the case of this cylindrical capacitor, after removing the casing, and unrolling its layers, there are two parallel metal sheets (here kept a fixed distance apart by an oil-impregnated sheet). (Video link: "MAKE presents: The Capacitor.")

The basic model of a capacitor is very similar, with two parallel metal plates of equal area A, held a fixed distance d apart. To keep things simple we assume that the space between the plates is air (or vacuum, although this space could be filled by an insulating liquid or solid "dielectric").

We can calculate the capacitance of a given parallel-plate capacitor from its area A and separation distance d. As the constant k has units of coulombs² per joule (C²/J) that remain after canceling out the A and d units, we redefine the C²/J units of capacitance as farads (F).

The capacitance of a capacitor is fixed once it is constructed, as the only way to change the capacitance is to change its "build" parameters: the area A and/or the separation distance d.

Now let's charge up a capacitor. This is done by connecting the capacitor plates to a voltage source such as a battery, in order to create a potential difference (in volts). As discussed in a previous presentation, electrons are the only mobile charges in a conductor, so only they are free to move, while the positively charged atomic nuclei remain fixed. Each and every electron taken from the top plate makes the top plate increasingly positively charged, and each and every one of these electrons are eventually deposited onto the bottom plate, making the bottom plate increasingly negatively charged. After the capacitor is fully charged, no more electrons can be moved, and the top and bottom plate have the same final charge of +Q and –Q.

So just how much charge could a capacitor store on its plates? When does a capacitor "know" when to stop charging?

Capacitance is the key relation between how much potential difference (voltage) is applied to the plates, and how much charge will finally be stored.

(The units for charge (in coulombs, C) and potential (in volts, V; or joules/coulomb, J/C) again work out to coulombs² per joule, or farads for the capacitance.)

The key is to realize that the capacitance of a capacitor, once built, is fixed. However, one can change the amount of potential applied to the capacitor (by connecting different batteries, etc.). With a given value of capacitance, then applying a high potential to the capacitor will allow it to store more charge, and applying a low potential to the capacitor will have it store less charge.

Thus capacitance can be said to be a measure of "charge-storing efficiency" with respect to a given potential, in that a large capacitance capacitor will store more charge than one with a small capacitance, if they are connected to the same potential source (such as a battery).

Capacitance is a critical parameter, as seen by disassembling a supposed ginormous 6,800 µF capacitor (which would store a lot of charge when connected to a given battery), and finding a cheaper 2,200 µF capacitor inside, which would store a lot less charge. What's up with that? ("KIRF" = "keeping it real fake.")

Second, storing electric potential energy in capacitors.

Let's watch a capacitor being charged, by applying a potential source to it (such as a battery), and watching the electrons removed from the top plate (making it positively charged) being deposited onto the bottom plate (making it negatively charged). Note how the first electron q travels quickly because it's "easy" to move, while the last electron q moves very slowly because it's "hard" to move.

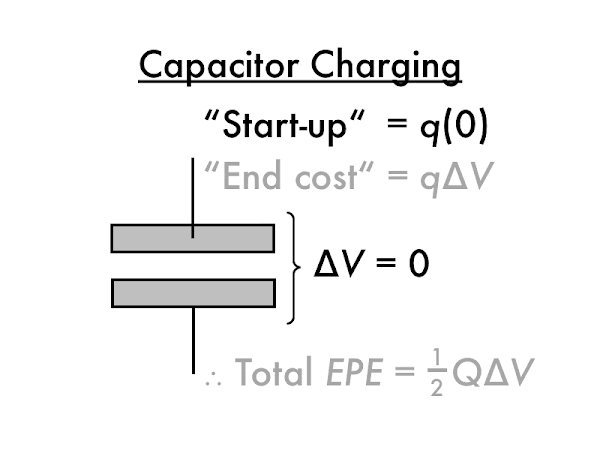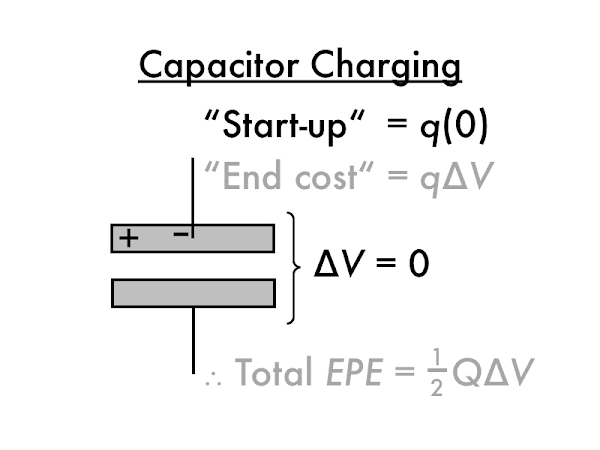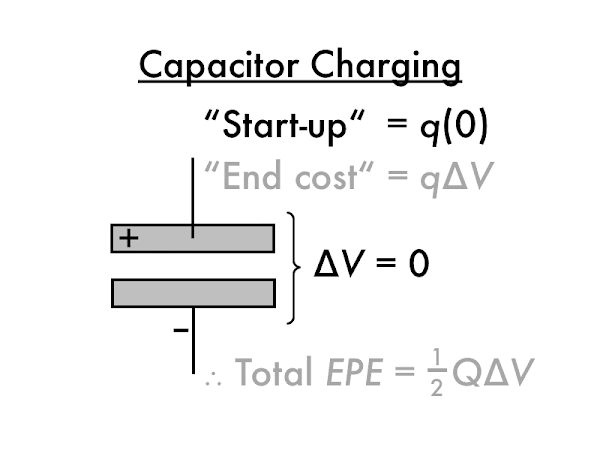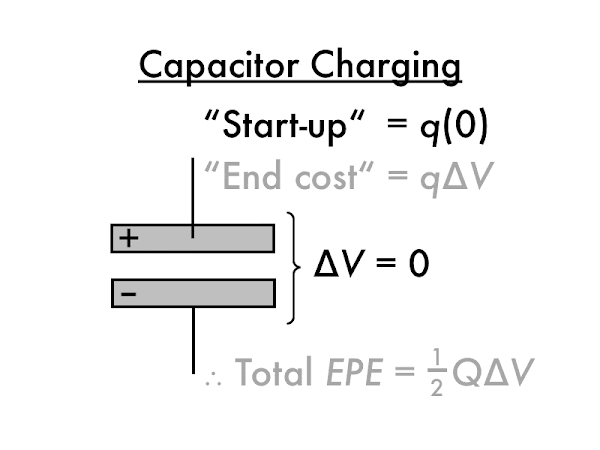
The first electron q has a "start-up" energy cost of effectively zero, as it moved from and to plates that are nearly or effectively uncharged (and start with zero potential, such that ∆EPE = q·(0) = 0 J).

However, the last electron q must be removed from a very positively charged plate, which requires a lot of work, and also must be moved onto a very negatively charged plate, again requiring a lot of work (the difficulty of which is indicated by the slowness of moving this electron). Since the plates are at or nearly at their final potential value ∆V, the last electron q has an energy "end cost" of ∆EPE = q·∆V (don't worry about negative signs in this argument).

Thus the first electron moved costs nothing (or nearly nothing), while the last electron requires a much higher q·∆V cost to move. The average cost of moving each electron, then, can be said to be (1/2)·q·∆V, such that the total cost of moving all electrons is (1/2)·Q·∆V, where the total charge of all N electrons moved is Q = N·q. (This argument is deliberately trying to avoid calculus to integrate the gradually increasing cost of each electron over all electrons moved, but the result is the same.)

So capacitors store electric potential energy by storing a given amount of charge when connected to a potential source (such as a battery). With the C = Q/∆V relation, the two parameters Q and ∆V in the electric potential energy equation can each be substituted out, yielding two other equivalent equations for electric potential energy EPE.

Endless hours of amusement await you when solving capacitor energy problems, so use caution when you use these equations, and more importantly, use only the equation you really need.

As in shock-deterrent clothing, capacitors are used to store electric potential energy to be used at a later time, such as camera flashes and this cardiac defibrillator. Sure, when you get "shocked" by a capacitor, charges are coming off of the capacitor (and traveling through your body), but it is the electric potential energy carried by these charges that makes capacitors hazardous. And more importantly, a key advantage capacitors have over batteries in storing electric potential energy for later use, is that the energy from a capacitor can be released in a very brief amount of time (as opposed to a small steady amount over a long period of time), as we will see in a subsequent presentation.