Online reading assignment: ideal fluid flow

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on ideal fluid flow.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"I understand that the flow rate or something is the speed at which something moves. I believe that thing is a liquid."

"The presentation preview introduces ideal fluid flow. An ideal fluid is incompressible, laminar, and non-viscous. Since it is incompressible, volume flow rate is conserved. Even if a pipe changes radius, the incompressibility of an ideal fluid means that the same volume flowing in one end must equal to the same volume coming out the other end in the same amount of time."

"When a fluid is traveling with a given speed and velocity through a given area, if it encounters a constriction (smaller area) then the velocity will increase and the pressure will decrease. The continuity equation relates time, flow area and distance traveled of a fluid, and Bernoulli's Equation relates pressure and velocity."

"I understand how volume flow rate past any two points is constant no matter the size of the cross-sectional area as long as the time interval is same for both points."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I found the math equations that go along with finding out the flow rate to be confusing."

"The equations were fine but its applications kind of confused me."

"I don't understand Bernoulli's equation. Nor do I get how to apply Bernoulli's principle."

"Need more explanations regarding the flow of an ideal fluid passing through increasing/decreasing area."

"I don't understand Bernoulli's equation, specifically how each term relates to the other."

What is the SI (Système International) unit for volume flow rate?

"m³/s."

"Q."

"meters-squared over seconds."

For an ideal fluid flowing through a pipe with a constant cross-sectional area, the volume flow rate ∆V/∆t:

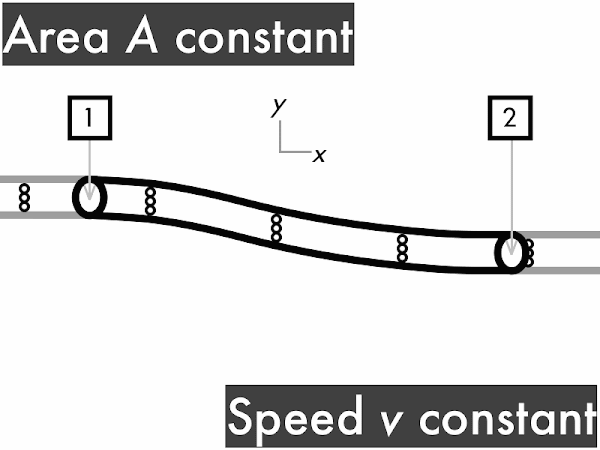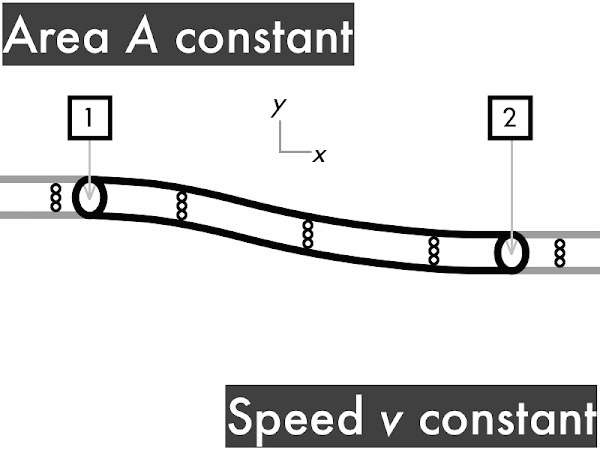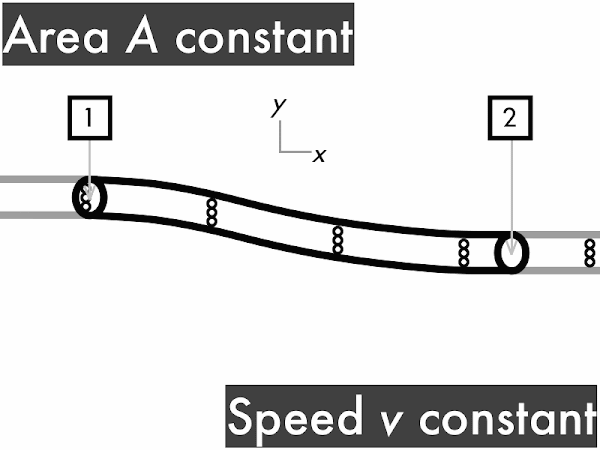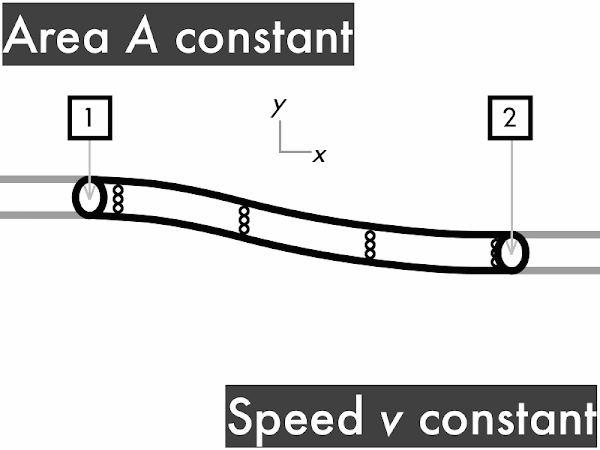
decreases.	** [2]
remains constant.	************************************************* [49]
increases.	***** [5]
(Unsure/lost/guessing/help!)	***** [5]

For an ideal fluid flowing through a pipe with an increasing cross-sectional area, the volume flow rate ∆V/∆t:

decreases.	*************************** [27]
remains constant.	********************** [22]
increases.	******** [8]
(Unsure/lost/guessing/help!)	**** [4]

For an ideal fluid flowing through a pipe with a decreasing cross-sectional area, the volume flow rate ∆V/∆t:

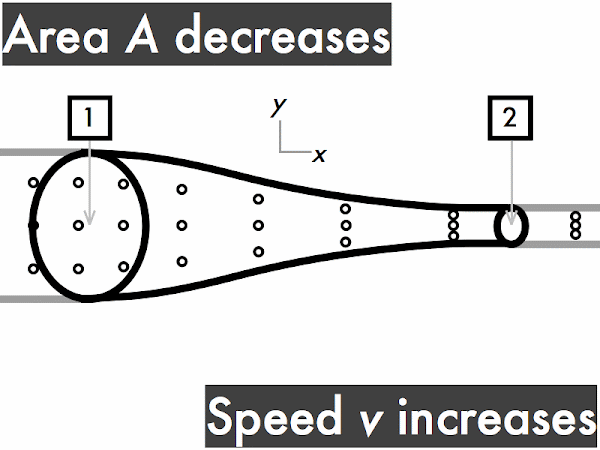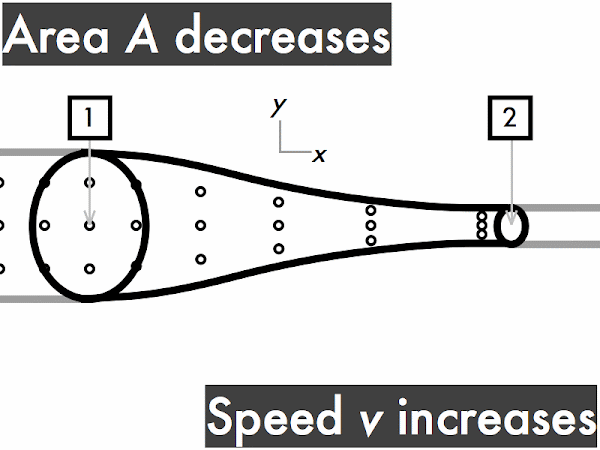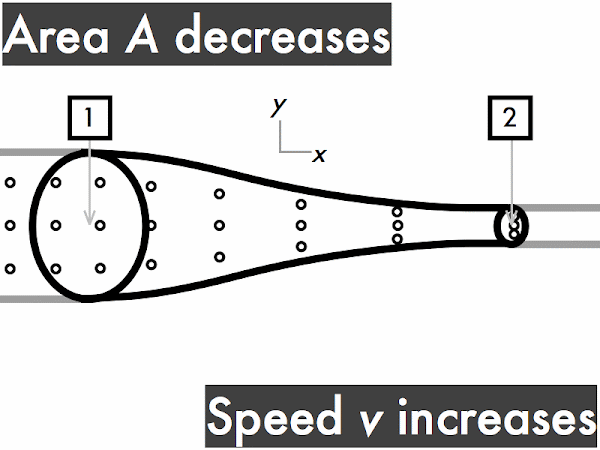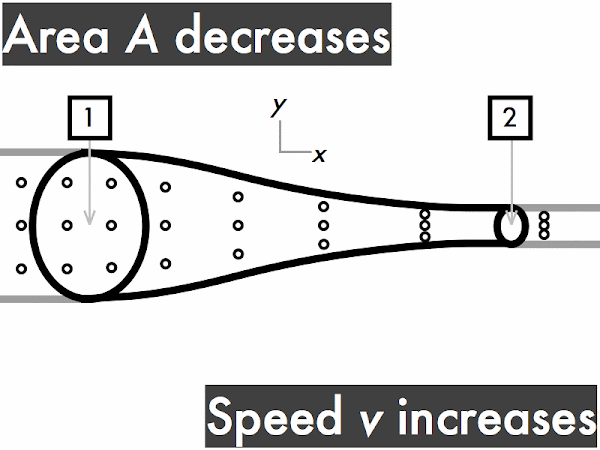
decreases.	********** [10]
remains constant.	***************** [17]
increases.	****************************** [30]
(Unsure/lost/guessing/help!)	**** [4]

For an ideal fluid flowing through a pipe with a widening cross-sectional area, indicate the changes in each of fluid flow parameters.
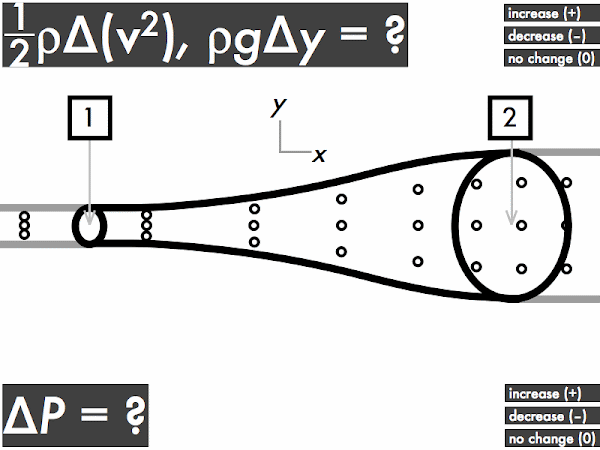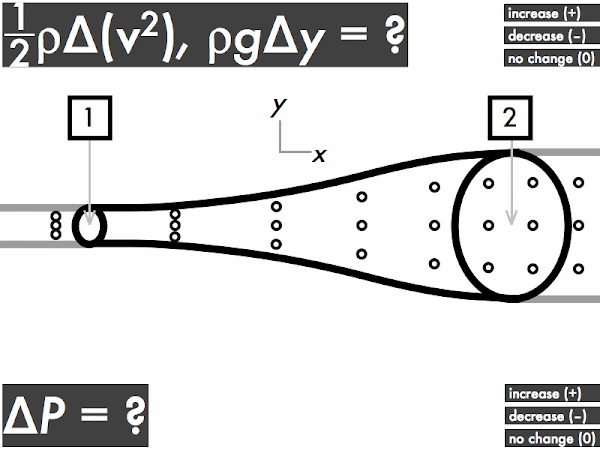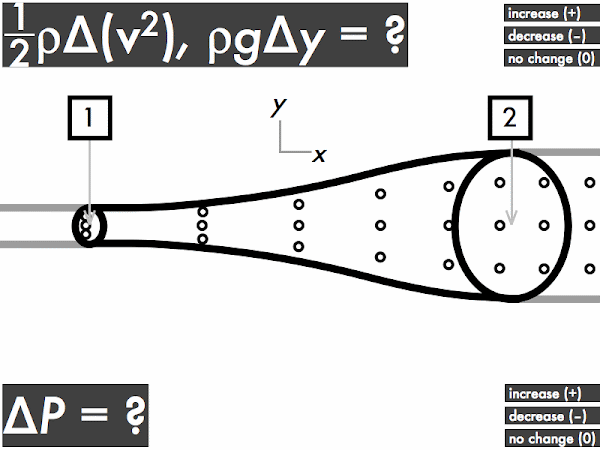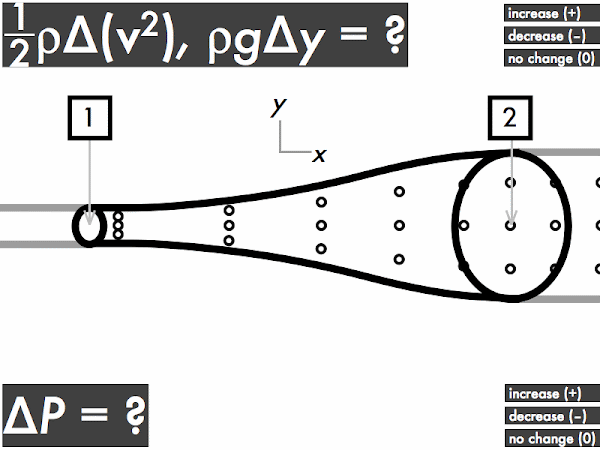
(Only correct responses shown.)

(1/2)·ρ·∆(v²) : decreases [44%]
ρ·g·∆y: no change [36%]
∆P: increases [23%]

For an ideal fluid flowing through a pipe with a narrowing cross-sectional area, indicate the changes in each of fluid flow parameters.
(Only correct responses shown.)

(1/2)·ρ·∆(v²) : increases [38%]
ρ·g·∆y: no change [31%]
∆P: decreases [23%]

For an ideal fluid flowing through a descending pipe with a constant cross-sectional area, indicate the changes in each of fluid flow parameters.
(Only correct responses shown.)

(1/2)·ρ·∆(v²) : no change [66%]
ρ·g·∆y: decreases [56%]
∆P: increases [66%]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"What's the difference between p, ρ and P?" ((Lower-case "p" is reserved for momentum; lower-case Greek letter rho "ρ" is reserved for density; and upper-case "P" is reserved for pressure. Don't even get started on how to denote power...)

"I hope you go over these GIF animations in class." (I will, and I hope you will understand them afterwards.)

"Sometimes I have to input answers twice for lab, homework and reading assignment due to my internet being crappy. When that happens, do you see only my last submission or do you get all of them?" (Most of the time I should see all of your multiple submissions, but will give you credit even if you split answers across different instances.)

"I wish the book would pull apart the equations more. It just gives it to us and doesn't explain what is what in relation to the concept we just learned." (This is nearly every textbook. Some more than others.)

"I always thought that fluid pressure increased when it is forced through a smaller area. Mind blown."