Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Problems 8.59, 8.60

University of Minnesota Physics Lecture Demonstrations
groups.physics.umn.edu/demo/mechanics/1Q1035.html
 A large ring has twice the radius and twice the mass as a small ring. They are both released from rest, and roll the same distance without slipping down the same ramp. Discuss why the large ring and the small ring will have the same translational speed at the bottom of the ramp. Neglect friction and drag. Explain your reasoning using the properties of rotational inertia, energy forms, and conservation of energy.
A large ring has twice the radius and twice the mass as a small ring. They are both released from rest, and roll the same distance without slipping down the same ramp. Discuss why the large ring and the small ring will have the same translational speed at the bottom of the ramp. Neglect friction and drag. Explain your reasoning using the properties of rotational inertia, energy forms, and conservation of energy.(Given: Iring = M·R2.)
Solution and grading rubric:
- p:
Correct. Sets (a) up an energy conservation equation with changes in gravitational potential energy, translational kinetic energy, and rotational kinetic energy summing to zero (no non-conservative work) for (b) a ring rolling without slipping, and (c) notes that due to the radii and mass canceling out from all terms, the final translational speed is neither mass- nor radius-dependent, and thus the different mass and radius rings must have the same final translational speed at the bottom of the ramp. - r:
As (p), but argument indirectly, weakly, or only by definition supports the statement to be proven, or has minor inconsistencies or loopholes. Has misplaced or missing factors in algebra (typically missing change in gravitational potential energy), but shows how mass and radius cancels out to result in the same final translational speed for both rings. - t:
Nearly correct, but argument has conceptual errors, or is incomplete. Has missing energy term and/or rolling without slipping condition. - v:
Limited relevant discussion of supporting evidence of at least some merit, but in an inconsistent or unclear manner. At least some systematic quantitative approach to implement energy conservation for objects that roll without slipping. - x:
Implementation/application of ideas, but credit given for effort rather than merit. Appeal to some other approach other than energy conservation, or states qualitatively how mass and/or radius will cancel out without explicitly showing how/why this should be so. - y:
Irrelevant discussion/effectively blank. - z:
Blank.
Sections 70854, 70855, 73320
Exam code: midterm02j0R6
p: 15 students
r: 6 students
t: 15 students
v: 10 students
x: 19 students
y: 1 student
z: 1 student
A sample "p" response (from student 0817), inadvertently dropping the g·(yf − y0) factor:
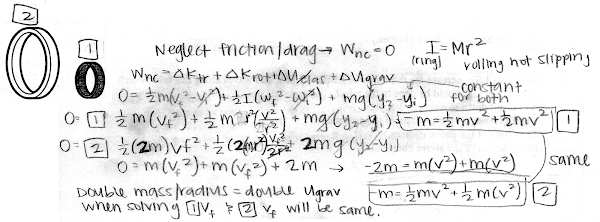
No comments:
Post a Comment