
Look at this diamond. Just look at it. All shiny and sparkly.
Realize that when we say it's "shiny" and "sparkly," we're not only looking at the light reflected off of the facets cut into the front surface of the diamond, but also the light reflected off of the facets cut into the back surface of the diamond--which means light within the diamond is reflecting off of a "surface of air!" (Video link: "
GIA Diamond - Sparkle scintillation under spot light, 0.75ct, M, Ex Vg Vg, MED.")

More conventionally, this fish as seen underwater is another example of how under certain conditions, light can be reflected off of the "surface of air" above.

In a
previous presentation we described how light is redirected at surfaces to undergo (specular) reflection, or refraction. Here we will extend the concept of refraction (and Snell's law) to describe how light undergoes
total internal reflection.

First, let's discuss three possible situations for a ray of light starting in a higher refractive index material, and the two conditions necessary for TIR to occur, which can be considered "frustrated refraction."
Keep in mind that total internal reflection (or TIR, for short) occurs only under certain conditions, but when it does occur light will behave as it does according to conventional specular reflection.
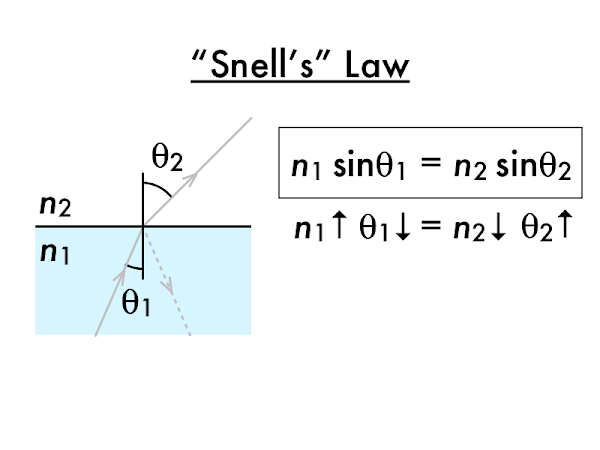
A necessary, but not sufficient condition for TIR to occur is for a ray of light in a higher refractive index material
n1 to be incident on a material with a lower refractive index material
n2. In this non-TIR case, since the light ray is transmitted out into the lower refractive index material, then the incident and transmitted angles θ
1 and θ
2 will merely be subject to Snell's law.

Now consider when the incident angle θ
1 (in the higher refractive index material
n1) is such that the transmitted angle θ
2 (in the lower refractive index material
n2) is 90°. When this occurs, the incident angle θ
1 is said to be at its
critical angle value θ
c.
Snell's law still applies here, and can be used to solve for this critical angle in the higher refractive index material
n1 that would result in a transmitted angle of 90° in the lower refractive index material
n2. (Even though it's there mathematically, the resulting transmitted ray is not really visible, so don't go looking for that ray traveling along the interface. In fact,
all of the energy of the incident ray will be reflected back into the original material.)

To get to the sufficient condition for TIR, then consider the case where the incident angle θ
1 in the higher refractive index material
n1 is
greater than the critical angle value θ
c.
In this case, there will be no ray transmitted out into the lower refractive index material
n2, and the ray will instead be
totally internally reflected back down into the higher refractive index material
n1, subject to the law of reflection. (If you attempt to implement Snell's law here to find a transmitted angle θ
2 out in the lower refractive index material
n2, you should get a calculator error, which is a signal that the total internal reflection (and thus the law of reflection) applies here, instead of Snell's law).

So in summary we have three possible cases if light starts in a higher refractive index material
n1:
- If the incident angle θ1 is less than the critical angle θc, then Snell's law applies, and can be solved to find the transmitted angle θ2 out in the lower refractive index material n2.
- If the incident angle θ1 is equal to the critical angle θc, then the transmitted angle θ2 = 90° out in the lower refractive index material n2. (Snell's law still applies here, typically to solve for the value of the critical angle θc.)
- If the the incident angle θ1 is greater than the critical angle θc, then the ray will be totally internally reflected back into the higher refractive index material n1, and the law of reflection applies (while Snell's law would not).
In this sense TIR is "frustrated refraction," as using Snell's law to solve for the transmitted angle in the lower refractive index material
n2 when θ
1 > θ
c would fail, leaving only the law of reflection applicable here.
We can also summarize the two conditions for TIR to occur:
- n1 > n2: a ray of light in a higher refractive index material n1 is incident on a material with a lower refractive index material n2.
- θ1 > θc: the incident angle in the higher refractive index material is greater than the critical angle value θc = sin-1(n2/n1).
If these two conditions are satisfied, then the ray will be total internally reflected back into the higher refractive index material.

Second, some applications of TIR.

An optical fiber allows a light signals to travel for great distances with a minimum loss of strength. Note that although coating the outside of a long glass tube with a reflective mirrored surface would also keep the light bouncing inside of the glass, with the right angle and refractive index every time the light hits this sides, it is incident at angle greater than the critical angle, and TIR occurs, keeping the light from escaping out into the lower refractive index surroundings.

This allows light to travel along optical fibers even if the fibers are not completely straight.

Bundling optical fibers together will allow images to be transmitted through from one end to the other, allowing doctors to see inside of nooks and crannies in our bodies...

...and plumbers to see inside of nooks and crannies inside our houses. (Video link: "
Ridgid See Snake Instructions.")

Back to our shiny and sparkly diamond. With cheap rhinestone imitations, the lower surfaces of rock crystals are coated with metal powder to force light from above to be reflected back upwards. However, a "brilliant cut" diamond has been shaped in a certain way...

...such that light from above will be totally internally reflected back upwards by the diamond-air interface at the bottom (sometimes totally internally reflecting many times before exiting out the top), with nothing on the lower surface but air! (Video link: "
Diamond.gif.")















No comments:
Post a Comment