Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 1/e, Problem 8.36
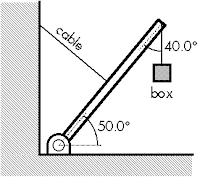[20 points.] A box is suspended by a uniform boom, of length 2.20 m and weight 80.0 N, as shown at right. A cable is attached perpendicular to the boom at its midpoint, and has a breaking strength of 200 N. What is the maximum weight of the box that can be suspended by this system before the cable breaks? Show your work and explain your reasoning.Solution and grading rubric:
- p = 20/20:
Correct. Sums all torques to zero (or sets counterclockwise torque of cable equal to the clockwise torques of the boom's weight, and the box) with lever arms measured from the pivot point to find that the maximum weight of the box is 116 N. - r = 16/20:
Nearly correct, but includes minor math errors. Applies rotational equilibrium condition to the boom, and at least recognizes and attempts to systematically calculate these three torque terms. - t = 12/20:
Nearly correct, but approach has conceptual errors, and/or major/compounded math errors. Attempts to apply rotational equilibrium, but one missing torque out of those exerted by the cable, weight of the boom, and weight of the box. - v = 8/20:
Implementation of right ideas, but in an inconsistent, incomplete, or unorganized manner. Some attempt at applying equilibrium condition to forces or components of forces. - x = 4/20:
Implementation of ideas, but credit given for effort rather than merit. - y = 2/20:
Irrelevant discussion/effectively blank. - z = 0/20:
Blank.
Grading distribution:
p: 5 students
r: 15 students
t: 8 students
v: 6 students
x: 2 students
y: 0 students
z: 0 students
A sample of a "p" response (from student 1468) is shown below:
Another "p" response (from student 2102):
An "r" response (from student 5913), recognizing the clockwise and counterclockwise torques that must be set equal to each other (but confusing the force of the 200 N tension cable with its torque):
No comments:
Post a Comment