Online reading assignment: ideal fluid flow

Physics 205A, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students have a bi-weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on ideal fluid flow.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"This section was mostly about flow rates the the motion of fluids. Since most fluids are incompresiable, they can be used in the equation of continuity because the mass flow rate is equal throught a tube. Bernoulli's equation links fluids and energy together."

"The difference between compressible/incompressible fluids. That water flow can be either laminar or turbulent."

"We are now going over fluid in motion. When water is going through a pipe at a certain speed it exits the pipe at that same rate and volume. If the water is flowing from a narrow opening to a larger opening, then the water will go from a faster speed to a slower speed as it flows from one area to the next. And the same for the other way around."

"How the flow of ideal fluid works and how it relates to volume and speed and whatnot. The more fluid crammed into a smaller area yields increased velocity."

"I understood from the blog was the description of ideal fluids. Ideal fluids are incompressible, laminar, and non-viscous."

"Steady flow is when a fluid has the same velocity from one point to the other, but it can still be steady while the velocity changes after that point if it still is constant. I understand that 'ρ' = fluid density, 'A' = cross-sectional area of tube, and 'v' = fluid speed."

"Ideal fluids are not compressible and also have a laminar flow, where the particles flow together side by side making for an easy movement, and should also have a non-viscous flow. With a changing radius of a tube holding water, the volume of the water does not change, however if the radius of a tube increases, then the speed will decrease."

"I understand the concept of increasing area means decreasing speed and vice versa when it comes to flowing fluids. This is easy for me because I learned it in physiology with blood flowing in blood vessels."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"Knowing how to whether/if cross-sectional area and speed is constant at a time and place."

"Volume flow conservation is confusing, in how it works with volume and time."

"Does pressure increase as the radius of a pipe pumping water decreases?"

"I would like to go over Bernoulli's equation and some problems to practice its application. Some of the terms in it were a bit confusing to follow. I feel good about the concept of how fluid flows through a pipe, but it is confusing when it starts being put in the equation."

"The second conservation law (Bernoulli's equation) for ideal fluids is somewhat confusing to me. The equation seems pretty difficult for me."

"I was confused with Bernoulli's conservation equation. I'm confused on how to relate static fluids with ideal fluids."

"Not sure how the gravitational potential energy density term is involved in ideal fluids."

"I thought pressure within the system should not change?"

"I'm not really sure when you use the volume flow conservation equation."

"The last few questions putting all of the terms together in Bernoulli's equation confused me. I don't understand the changes in pressure in connection with the area and speed changes."

"Just number examples, homie."

"I found nothing confusing."

What is the SI (Système International) unit for volume flow rate?

"Meters cubed per second."

"m³/s."

"Cubic meters per second."

"m³/s = Pascals?"

"J/m³?"

"kg/s?"

"The SI unit for volume flow rate is inches and yards?"

For an ideal fluid flowing through a pipe with a constant cross-sectional area, the volume flow rate ∆V/∆t:

decreases.	* [1]
remains constant.	***************************************** [41]
increases.	[0]
(Unsure/lost/guessing/help!)	* [1]

For an ideal fluid flowing through a pipe with an increasing cross-sectional area, the volume flow rate ∆V/∆t:

decreases.	*********************** [23]
remains constant.	********* [9]
increases.	******** [8]
(Unsure/lost/guessing/help!)	*** [3]

For an ideal fluid flowing through a pipe with a decreasing cross-sectional area, the volume flow rate ∆V/∆t:

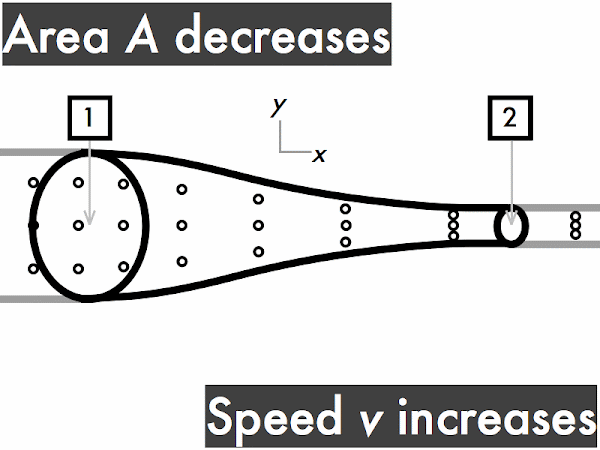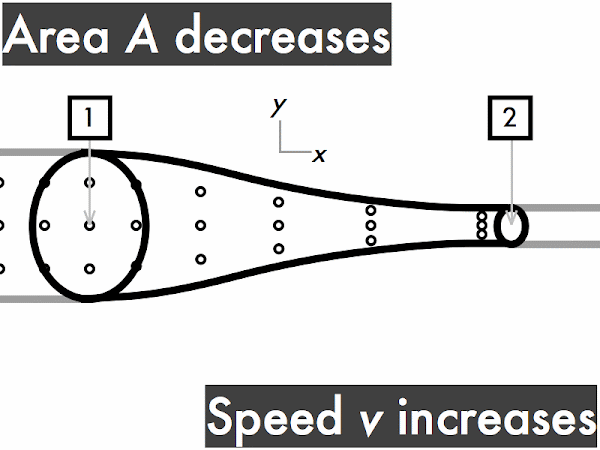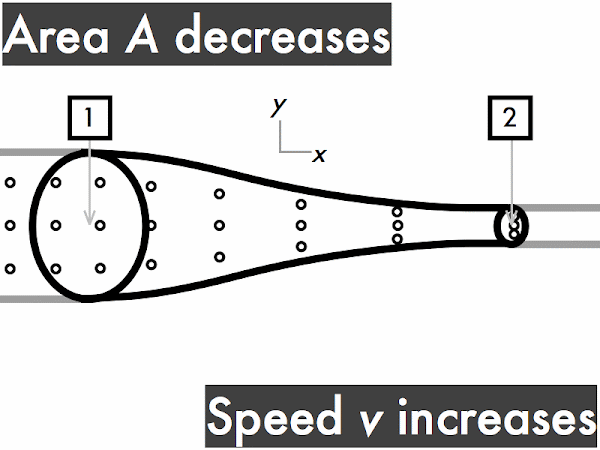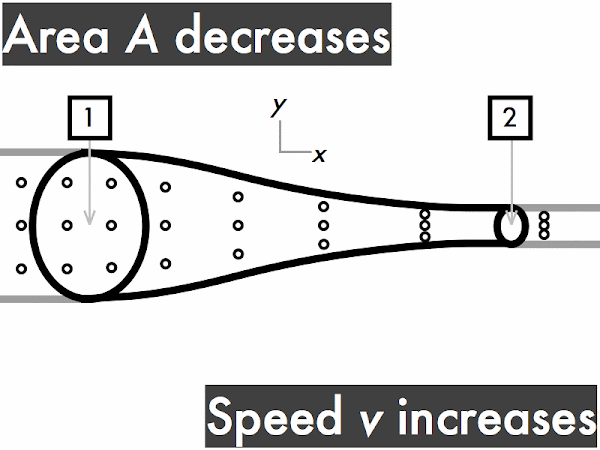
decreases.	********* [9]
remains constant.	********** [10]
increases.	********************** [22]
(Unsure/lost/guessing/help!)	** [2]

For an ideal fluid flowing through a horizontal pipe with a widening cross-sectional area, indicate the changes in each of fluid flow parameters.
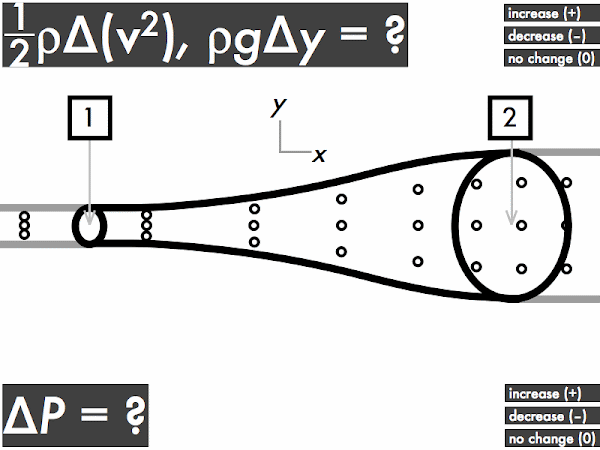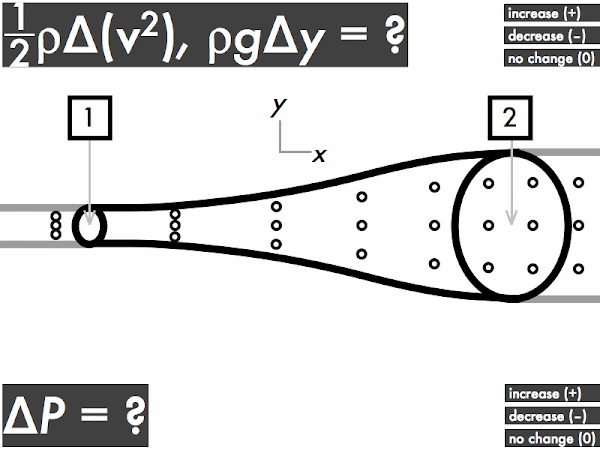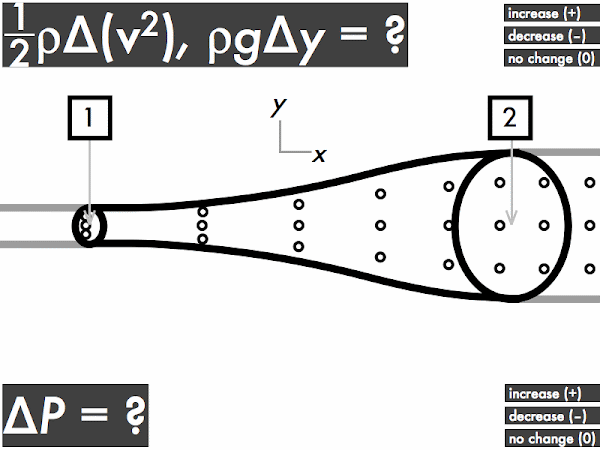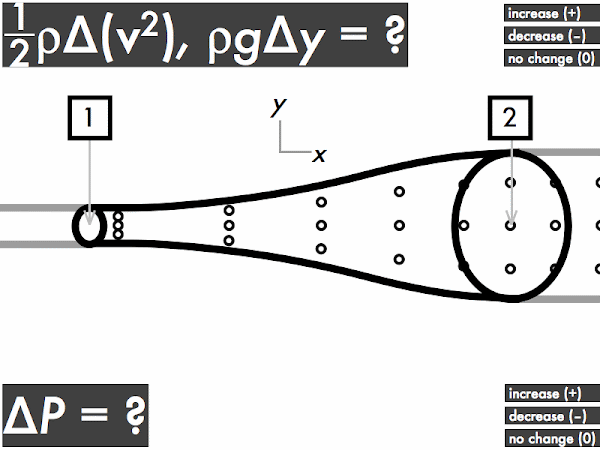
(Only correct responses shown.)

(1/2)·ρ·∆(v²): decreases [40%]
ρ·g·∆y: no change [33%]
∆P: increases [21%]

For an ideal fluid flowing through a horizontal pipe with a narrowing cross-sectional area, indicate the changes in each of fluid flow parameters.
(Only correct responses shown.)

(1/2)·ρ·∆(v²): increases [42%]
ρ·g·∆y: no change [30%]
∆P: decreases [56%]

For an ideal fluid flowing through a descending pipe with a constant cross-sectional area, indicate the changes in each of fluid flow parameters.
(Only correct responses shown.)

(1/2)·ρ·∆(v²): no change [70%]
ρ·g·∆y: decreases [12%]
∆P: increases [7%]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Isn't water at the bottom of the ocean more compressed that water on the surface would that make it technically compressible?" (Yes, according to the European Space Agency, the increase in water density is approximately 4% in the deepest parts of the ocean (the Marianas Trench), but since most of our calculations only have two significant figures, then for our purposes water can be considered incompressible.)

"How should we be keeping track of all these equations, in these last few weeks we have gotten like 10 new ones?" (At the bottom of the practice quizzes (also on the last page of the worksheet packets), label each variable, and summarize each equation. This is the vocabulary and language of physics, so it will take some time to become fluent, by using these equations in the homework.)

"Can we go over the water flowing through widening and narrowing cross-sectional areas and ascending/descending pipes?" (Yes. But thanks for trying--sometimes I don't realize how difficult things are going to be until I make you try them out.)

"How does the ∆y term figure into the conservation equations for ideal fluid flow?" (For static fluids, a decrease in height (making ∆y negative) corresponded to an increase in pressure (making ∆P positive). For ideally flowing fluids, the increase or decrease in ∆y must be tied to both changes in pressure (∆P) and changes in kinetic energy density ((1/2)·ρ·(∆v²). This is essentially like using the transfer-balance energy conservation equation with no non-conservative work (making the left-hand side of the equation zero), and three (or more) energy change terms on the right-hand side.)

"So when cross-sectional area decreases, it increases the speed and pressure of the fluid?" (Assuming that the pipe is horizontal, yes, the speed increases, but there must be a corresponding decrease in pressure. We'll cover this in more detail in class.)

"How can I pass this class?" (See me during office hours. We'll go through your individual case and break it down for you.)

"No questions."

"No comment."

"Uhh."

Physics quiz question: shortening length of guitar string

Physics 205A Quiz 6, fall semester 2014
Cuesta College, San Luis Obispo, CA

Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Conceptual Question 11.4, Multiple-Choice Question 11.5

For a standard guitar the B3 string vibrates at a fundamental frequency of 247 Hz with a tension of 40.5 N. The string is 0.648 m long[*]. A capo is a device that is attached to this guitar to shorten the length of the B3 string, which would then have a fundamental frequency __________ 247 Hz.
(A) lower than.
(B) equal to.
(C) higher than.
(D) (Not enough information is given.)

[*] "Gauge: 8-38 Standard Set," jemsite.com/forums/f21/string-tension-charts-73846.html.

Correct answer (highlight to unhide): (C)

The speed of waves along the string is given by:

v = √(F/(m/L)).

Shortening the length of the string that vibrates would not change the linear mass density m/L (as there would be proportionally less mass for a shorter string length), and since the tension F would also be unchanged, then the speed v of waves that travel along the string remains constant.

The fundamental frequency of a standing wave on a string is given by:

f₁ = v/(2·L),

and since decreasing the length L of the string, while leaving the wave speed v unchanged, would result in an increase in the f₁ frequency.

Sections 70854, 70855
Exam code: quiz06eAg7
(A) : 4 students
(B) : 3 students
(C) : 57 students
(D) : 0 students

Success level: 89%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.33

Physics quiz question: Houston Museum of Natural Science pendulum cable length

Physics 205A Quiz 6, fall semester 2014
Cuesta College, San Luis Obispo, CA

"Foucault Pendulum @ Houston Museum of Natural Science"
pincam23
youtu.be/WfqsfMu4VKc

A pendulum set up at the Houston Museum of Natural Science[*] has a mass of 81.6 kg and swings back-and-forth with a period of 8.71 s. Ignore friction/drag. The length of the pendulum cable is:
(A) 5.1 m.
(B) 5.9 m.
(C) 9.6 m.
(D) 19 m.

[*] youtu.be/nB2SXLYwKkM.

Correct answer (highlight to unhide): (D)

The period of a pendulum is given by:

T = 2·π·√(L/g),

which does not depend on the mass. Since the period T = 8.71 s and gravitational constant g = 9.80 m/s² are known, the length L can then be solved for:

L = g·(T/(2·π))²,

L = (9.80 m/s²)·((8.71 s)/(2·π))² = 18.8514856 m,

or to two significant figures, the length of the pendulum cable is 19 m.

(Response (A) is g·((2·π)/T)²; response (B) is 2·π·√(T/g); response (C) is √(m·g/T).)

Sections 70854, 70855, 73320
Exam code: quiz06eAg7
(A) : 3 students
(B) : 4 students
(C) : 5 students
(D) : 52 students

Success level: 81%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.53

Physics quiz question: energy changes of block sliding up wall

Physics 205A Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

A sanding block is pressed against the wall, and slides up at constant speed as a diagonal force is applied to it. The wall is not frictionless. The __________ of the block remains constant as it slides up the wall.
(A) gravitational potential energy.
(B) translational kinetic energy.
(C) (Both of the above choices.)
(D) (Neither of the above choices.)

Correct answer (highlight to unhide): (B)

The energy transfer-balance equation is given by:

W_nc = ∆KE_tr + ∆PE_grav + ∆PE_elas,

where ∆PE_elas = 0, as there is no spring involved in this process.

Just looking at the two remaining terms on the right-hand side of the energy transfer-balance equation, for the change in translational kinetic energy:

∆KE_tr = (1/2)·m·(v_f² – v₀²),

and since the speed is constant, v₀ and v_f have the same magnitude, then KE_tr is constant (∆KE_tr = 0).

Also for the change in gravitational potential energy:

∆PE_grav = m·g·(y_f – y₀),

and since y_f is greater than y₀, then PE_grav increases (∆PE_grav is positive).

Sections 70854, 70855, 73320
Exam code: quiz04th1R
(A) : 6 students
(B) : 37 students
(C) : 5 students
(D) : 3 students

Success level: 73%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.64

Physics quiz question: comparing BASE jumper energy changes

Physics 205A Quiz 4, fall semester 2016
Cuesta College, San Luis Obispo, CA

"KL tower base jump 2012 | Kuala Lumpur | Malaysia"
enshahdi
flic.kr/p/df5Nwd

A "BASE[*]" jumper (total mass of 88 kg with equipment) reached a final terminal speed of 53 m/s after falling 452 meters downwards (before using his parachute)[**]. Drag is not negligible, assume a zero initial speed, and that he dropped straight down. For this process, the decrease in gravitational potential energy of the jumper was __________ the increase in translational kinetic energy of the jumper.
(A) less than.
(B) equal to.
(C) greater than.
(D) (Not enough information is given.)

[*] Jumping off of a "building, antenna, span, or Earth (i.e., cliff)."
[**] johnnyutah.com/freefallchart1.html.

Correct answer (highlight to unhide): (C)

The energy transfer-balance equation is given by:

W_nc = ∆KE_tr + ∆PE_grav + ∆PE_elas,

where ∆PE_elas = 0, as there is no spring involved in this process. Note that on the left-hand side of this equation, the non-conservative work done by the non-neglible drag force against the BASE jumper is:

W_nc = (F_drag·cosθ)·s,

and must have a negative value, as the tail-to-tail angle between the upwards drag force and the downwards displacement is θ = 180°, and cos(180°) = –1. (Note that the weight force on the BASE jumper is a conservative force, and is already included in the ∆PE_grav term on the right-hand side of the equation, so the work done by this force is not explicitly considered here.)

Since the left-hand side of the energy transfer-balance equation is negative, then:

(–) = ∆KE_tr + ∆PE_grav,

such that decrease in gravitational potential energy (∆PE_grav is negative) must be greater than the increase in translational kinetic energy (∆KE_tr is positive).

Sections 70854, 70855, 73320
Exam code: quiz04th1R
(A) : 13 students
(B) : 16 students
(C) : 22 students
(D) : 0 students

Success level: 43%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.82

Physics quiz question: tractor-trailer crash impulse

Physics 205A Quiz 4, fall semester 2016
Cuesta College, San Luis Obispo, CA

"Fig. 4.59. Sloshing of Tractor-Trailer Cargo (Right View)"
Texas A&M Transportation Institute
tti.tamu.edu/documents/9-4973-1.pdf

A computer simulation of a tractor-trailer vehicle (mass of 3.5×10⁴ kg) colliding at a speed of 22 m/s with a stationary concrete bridge support predicts that it takes 0.35 s to come to a complete stop[*]. If the concrete bridge support had "impact attenuators" (plastic barrels filled with sand[*]), the tractor-trailer vehicle would take a longer time to come to a complete stop. This would __________ the magnitude of the impulse exerted on the tractor-trailer vehicle.
(A) decrease.
(B) not change.
(C) increase.
(D) (Not enough information is given.)

[*] C. Eugene Buth, William F. Williams, Michael S. Brackin, Dominique Lord, Srinivas R. Geedipally, and Akram Y. Abu-Odeh, "Analysis of Large Truck Collisions with Bridge Piers: Phase 1. Report of Guidelines for Designing Bridge Piers and Abutments for Vehicle Collisions," Texas Transportation Institute (May 2010), p. 39, tti.tamu.edu/documents/9-4973-1.pdf.
[**] traffixdevices.com/products/attenuators.

Correct answer (highlight to unhide): (B)

The impulse J can be calculated as the initial-to-final change in momentum:

J = ∆p = m·∆v,

where ∆v = v_f – v₀.

The initial velocity vector is v₀ = +22.0 m/s (traveling in the forwards direction), and the final velocity vector is v_f = 0 m/s (coming to a complete stop). Then:

J = (3.5×10⁴ kg)·((0 m/s) – (+22.0 m/s)) = –770,000 N·s,

or to two significant figures, the magnitude of the impulse is 7.7×10⁵ N·s (and the "–" sign indicates that it is in the backwards direction).

If the same tractor-trailer with same initial velocity of +22.0 m/s instead collides with an "impact attenuator" and comes to a complete stop over a longer duration of time, the impulse on the tractor-trailer would be the same as colliding and coming to a stop without it. However, the longer duration of time to come to a complete stop in the case of the impact attenuator would decrease the net force on the tractor-trailer, as:

J = ΣF·∆t.

Sections 70854, 70855
Exam code: quiz04th1R
(A) : 32 students
(B) : 9 students
(C) : 10 students
(D) : 0 students

Success level: 18%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.16

Physics quiz question: classification of staged car collision

Physics 205A Quiz 4, fall semester 2016
Cuesta College, San Luis Obispo, CA

"Accident Reconstruction Example"
Evans Accident Reconstruction
evansar.com/example.html

A crash was staged[*] between a 1997 Pontiac Grand Am (mass 1.30×10³ kg[**]) traveling at 17 m/s and a stationary 1991 Volkswagen Jetta (mass 1.47×10³ kg[**]). Both cars sustained significant damage, and completely separated from each other after the collision. Ignore friction, drag, and external forces during this brief collision. This collision is:
(A) completely inelastic.
(B) (partially) inelastic.
(C) elastic.
(D) (None of the above choices.)

[*] evansar.com/example.html.
[**] thecarconnection.com/specifications/pontiac_grand-am_1997_4dr-sdn-se.
[***] automobile-catalog.com/make/volkswagen/jetta_2gen/jetta_2gen/1991.html.

Correct answer: (B)

Negligible net external force and brief time duration for this collision makes the external impulse on this system zero, such that momentum is conserved. Since both cars sustained significant damage, translational kinetic energy is not conserved, and so this collision cannot be elastic. As both cars separated from each other after the collision, this collision cannot be a completely inelastic collision, and this collision must then be classified as (partially) inelastic.

Sections 70854, 70855, 73320
Exam code: quiz04th1R
(A) : 2 students
(B) : 44 students
(C) : 4 students
(D) : 1 student

Success level: 86%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.36

Astronomy quiz question: absolute magnitude of Eta Aurigae from apparent magnitude, distance

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

Eta Aurigae is a star with an apparent magnitude of m = +3.2, and is located 75 parsecs from Earth. Eta Aurigae has an absolute magnitude M of:
(A) –1.2.
(B) +3.2.
(C) +4.4.
(D) Not enough information is given.)

Correct answer (highlight to unhide): (A)

Eta Aurigae appears to have a brightness of +3.2 as seen from its true distance of 75 parsecs from Earth, but when placed at the "fair" distance of 10 parsecs away (where it would have its "fair brightness" or absolute magnitude), Eta Aurigae would become brighter.

(Response (B) is the same magnitude as the given apparent magnitude; response (C) is dimmer than the given apparent magnitude.)

Section 70158
Exam code: quiz05s4nD
(A) : 19 students
(B) : 3 students
(C) : 2 students
(D) : 13 student

Success level: 54% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.30

Astronomy quiz question: absolute magnitude of Altair from apparent magnitude, distance

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

Altair is a star with an apparent magnitude of m = +0.8, and is located 5.1 parsecs from Earth. Altair has an absolute magnitude M of:
(A) –3.0.
(B) +0.8.
(C) +2.2.
(D) Not enough information is given.)

Correct answer (highlight to unhide): (C)

Altair appears to have a brightness of +0.8 as seen from its actual location of 5.1 parsecs from Earth, but when placed at the "fair" distance of 10 parsecs away (where it would have its "fair brightness" or absolute magnitude), Altair would become dimmer.

(Response (A) is brighter than the given apparent magnitude; response (B) is the same magnitude as the given apparent magnitude.)

Section 70160
Exam code: quiz05n0Ko
(A) : 6 students
(B) : 1 student
(C) : 11 students
(D) : 7 student

Success level: 49% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.63

Astronomy quiz question: Altair's absorption line blueshift

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

Altair is a star with an apparent magnitude of m = +0.8, and is located 5.1 parsecs from Earth. The absorption lines in Altair's spectrum are slightly blueshifted, indicating that Altair is:
(A) slightly cooler than expected.
(B) slightly warmer than expected.
(C) moving towards Earth.
(D) moving away from Earth.

Correct answer (highlight to unhide): (C)

Absorption lines that are "blueshifted" means that they have slightly shorter wavelength values than expected (shifting all of them slightly towards the blue end of the spectrum), such that Altair is moving towards Earth.

Section 70160
Exam code: quiz05n0Ko
(A) : 0 students
(B) : 1 student
(C) : 20 students
(D) : 4 students

Success level: 81% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.02

Astronomy quiz question: Eta Aurigae's absorption line redshift

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

Eta Aurigae is a star with an apparent magnitude of m = +3.2, and is located 75 parsecs from Earth. The absorption lines in Eta Aurigae's spectrum are slightly redshifted, indicating that Eta Aurigae is:
(A) slightly cooler than expected.
(B) slightly warmer than expected.
(C) moving towards Earth.
(D) moving away from Earth.

Correct answer (highlight to unhide): (D)

Absorption lines that are "redshifted" means that they have slightly longer wavelength values than expected (shifting all of them slightly towards the red end of the spectrum), such that Eta Aurigae is moving away from Earth.

Section 70158
Exam code: quiz05s4nD
(A) : 9 students
(B) : 2 students
(C) : 5 students
(D) : 21 students

Success level: 58% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.80

Astronomy quiz question: M0 supergiant vs. G0 giant

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

An M0 supergiant has a ___________ than a G0 giant.
(A) hotter temperature.
(B) brighter luminosity.
(C) larger size.
(D) (Two of the above choices.)
(E) (All of the above choices.)
(F) (None of the above choices.)

Correct answer (highlight to unhide): (D)

An H-R diagram is provided with this quiz.


These stars are plotted on an H-R diagram below. While the M0 supergiant has a cooler temperature, it has a brighter luminosity and a larger size than the G0 giant.


Section 70158
Exam code: quiz05s4nD
(A) : 4 students
(B) : 6 students
(C) : 6 students
(D) : 15 students
(E) : 2 students
(F) : 4 students

Success level: 46% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.80

Section 70160
Exam code: quiz05n0Ko
(A) : 0 students
(B) : 1 student
(C) : 7 students
(D) : 12 students
(E) : 2 students
(F) : 3 students

Success level: 52% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.59

Astronomy current events question: newer young dates for lunar surface features

Astronomy 210L, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Robert Burnham, "Small Impacts are Reworking the Moon's Soil Faster than Scientists Thought" (October 12, 2016)
asunow.asu.edu/20161012-asu-scientists-discover-moon-getting-hit-more-often

The moon may be impacted more frequently that previously thought, based on analysis of NASA's Lunar Reconnaissance Orbiter's:
(A) micrometeorite-induced damage.
(B) orbital fluctuations.
(C) radar reflections.
(D) surface images.
(E) crust samples.

Correct answer: (D)

Student responses
Sections 70178, 70186
(A) : 2 students
(B) : 0 students
(C) : 1 student
(D) : 17 students
(E) : 0 students

Astronomy current events question: larger estimate for galaxies in universe

Astronomy 210L, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Ray Villard, Mathias Jäger, and Christopher Conselice, "Hubble Reveals Observable Universe Contains 10 Times More Galaxies Than Previously Thought" (October 13, 2016)
hubblesite.org/newscenter/archive/releases/2016/39/full/

Over 90% of galaxies in the universe have yet to be detected, based on __________ of Hubble Space Telescope images.
(A) false-coloring.
(B) lookback times.
(C) 3-D modeling.
(D) dark matter densities.
(E) infrared filtering.

Correct answer: (C)

Student responses
Sections 70178, 70186
(A) : 5 students
(B) : 3 students
(C) : 5 students
(D) : 3 students
(E) : 4 students

Astronomy current events question: proposed Project Blue space telescope

Astronomy 210L, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Mary Beth Griggs
, "'Project Blue' Aims to Take the First Snapshot of a Twin Earth" (October 10, 2016)
popsci.com/project-blue-aims-to-be-first-to-image-planet-near-alpha-centauri

The proposed Project Blue space telescope will directly image Alpha Centauri star system exoplanets by:
(A) blocking star light.
(B) using interferometry.
(C) analyzing emission spectra.
(D) detecting gravity waves.
(E) recording Doppler shifts.

Correct answer: (A)

Student responses
Sections 70178, 70186
(A) : 14 students
(B) : 3 students
(C) : 1 student
(D) : 1 student
(E) : 1 student

Astronomy quiz question: B5 white dwarf vs. M0 red dwarf

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

A B5 white dwarf can have the same __________ as an M0 red dwarf.
(A) luminosity.
(B) size.
(C) temperature.
(D) (Two of the above choices.)
(E) (All of the above choices.)
(F) (None of the above choices.)

Correct answer (highlight to unhide): (A)

An H-R diagram is provided with this quiz.


These stars are plotted on an H-R diagram below. The B5 white dwarf has a higher temperature and a smaller size than the M0 red dwarf, but these two stars could have the same luminosity.


Section 70158
Exam code: quiz05s4nD
(A) : 16 students
(B) : 6 students
(C) : 3 students
(D) : 7 students
(E) : 1 student
(F) : 4 students

Success level: 46% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.30

Section 70160
Exam code: quiz05n0Ko
(A) : 9 students
(B) : 6 students
(C) : 1 student
(D) : 8 students
(E) : 0 students
(F) : 1 student

Success level: 42% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.09

Astronomy quiz archive: sun/spectra/star properties

Astronomy 210 Quiz 5, fall semester 2016
Cuesta College, San Luis Obispo, CA

Section 70158, version 1
Exam code: quiz05s4nD


Section 70158

0- 8.0   :	** [low = 4.0]
8.5-16.0 :	**
16.5-24.0 :	***************
24.5-32.0 :	********* [mean = 26.9 +/- 6.9]
32.5-40.0 :	******** [high = 36.5]

Section 70160, version 1
Exam code: quiz05n0Ko


Section 70160

0- 8.0 :	* [low = 8.0]
8.5-16.0 :	****
16.5-24.0 :	************
24.5-32.0 :	******************* [mean = 27.5 +/- 7.3]
32.5-40.0 :	*************** [high = 40.0]

Online reading assignment: fusion, nebulae, star cluster ages (SLO campus)

Astronomy 210, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on fusion, nebulae, and star cluster ages.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"Star life cycles--they say a million years is a short life, yet seems like a really long time for us."

"How the sun takes four hydrogen atoms and converts them into one helium atom and energy. This was interesting because when I was younger I just assumed that there was a bunch of gasoline in the sun supplying it with energy."

"How fusion releases energy."

"The birth of stars. Now I can school my fifth grade students with some astronomy they don't know [yet]."

"How dust similar in size to cigarette smoke creates a blue glow like cigarette smoke."

"I thought the different types of nebulae were totally wicked sweet. I thought it was cool how the dust clouds reflect blue light because the short wave lengths get scattered in all directions."

"I find all the different colors in the nebulae really interesting, because of what gives off theses different colors like the small and large particles of dust."

"I thought it was interesting to learn that there are only three nebulae colors."

"Emission nebula are just made out of hydrogen atoms and that is so simple but so amazing.."

"It all seems interesting but its very scienc-y and wordy to me. Once I understand it better I can find more of this interesting."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"Fusion confuses me."

"Why does fusion exist?"

"Fusion rates for different mass stars."

"Fusion...I just don't get it."

"The proton-proton chain, I did not understand how the sun and stars produce energy."

"Fusion. I do not like chemistry! Help!"

"The whole temperature, pressure, and fusion rate thing really confused me."

"The fact that not all stars obey the cheerleader model confused me."

"Honestly I feel like memorizing the facts on nebulae will be difficult."

"The turn-off point with star clusters"

"Most of this information seemed difficult to grasp through my own thought processes, but this is all normally cleared up by the time lecture is over tomorrow night."

"Everything was pretty easy to understand."

Rank the luminosities of these main-sequence stars (1 = brightest, 3 = dimmest). (There are no ties.)
(Only correct responses shown.)

Massive: brightest luminosity [88%]
Medium-mass (sunlike): medium luminosity [91%]
Low mass (red dwarf): dimmest luminosity [94%]

Rank the fusion rates of these main-sequence stars (1 = fastest, 3 = slowest). (There are no ties.)
(Only correct responses shown.)

Massive: fastest fusion rate [75%]
Medium-mass (sunlike): medium fusion rate [97%]
Low mass (red dwarf): slowest fusion rate [78%]

Fusion requires high temperatures in order for nuclei to move quickly enough to:

break heavy elements apart.	*** [3]
create convection currents.	** [2]
overcome gravity.	* [1]
overcome repulsion.	********************* [21]
(Unsure/guessing/lost/help!)	***** [5]

Briefly explain why "cold fusion" (producing energy from hydrogen fusion at room temperature) would be implausible.

"The hydrogen atoms would move too slow to overcome repulsion and collide with each other."

"The temperature is not high enough for hydrogen atoms to get squeezed and move quickly and will not result in a lot of them fusing together to release energy."

"During fusion, the temperature must be high, meaning high speeds, as this high temperature helps overcome the coulomb barrier that repels the two nuclei."

"In order for fusion to produce the energy from hydrogen it needs heat and the more the better it is at producing energy and fusing. Cold fusion is just not hot enough to do its thing."

"I did not get that part."

"Because we need such intense heat that the nuclei gets so hot that it almost melts together?"

Match the three different types of nebulae with their colors.
(Only correct responses shown.)

Emission: pink [75%]
Reflection: blue [81%]
Dark: brown/black [88%]

Match the three different types of nebulae with their composition.
(Only correct responses shown.)

Emission: hydrogen [84%]
Reflection: small dust particles [87%]
Dark: large dust particles [97%]

Rank the lifetimes of these main-sequence stars (1 = shortest, 3 = longest). (There are no ties.)
(Only correct responses shown.)

Massive: shortest main-sequence lifetime [67%]
Medium-mass (sunlike): medium main-sequence lifetime [93%]
Low mass (red dwarf): longest main-sequence lifetime [72%]

If there was an open invitation to a house party (no specific time given), when would you show up?

Early, or on time.	***** [5]
When the most people should be there.	*************************** [27]
After most everyone has left.	[0]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"How can I become a star in this class?" (Literally, or figuratively?)

"When does the International Space Station pass overhead next?" (Check out spotthestation.nasa.gov for your area.)

"Hopefully I pass this class." (I hope so, too.)

"What does fusion have to do with cheerleading? I still don't get that."

"You are my favorite teacher--I wish I had you more than one time a week."

Online reading assignment: static fluids

Physics 205A, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students have a bi-weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on static fluids.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"Pressure is the amount of force exerted over an area. This area can be on almost any surface such as a solid, liquid, or gas. The smaller the area the more pressure there is on it. However, it also goes the other way."

"I understand the units and how to convert. Chemistry helped me with this. I understand the basics of pressure and how altitude or being submerged could affect each."

"When you are going down in fluid the pressure will increase and when you are going up in a fluid the pressure decreases by change in p value. I can relate this to when you jump into a pool, the father you go down the more pressure there is and your ears begin to pop."

"The force over a certain area is what creates force density. The pressure can be also an energy per volume."

"I can connect with the reading because I dive regularly and am constantly having to account for pressure changes. Plus I'm a fan of hydrodynamics, so this is the tip of that iceberg."

"What I understood from the blog was buoyancy. The equation was a lot more clearer to me and how to use the complete volume of the object if it is totally submerged and to use part of the object volume that is submerged."

"I understood pretty much all of it. There was nothing that was too difficult. Calculating pressure and buoyancy seem to be pretty straightforward."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I didn't completely understand the styrofoam cup example. I don't know whether the pressure around the cups increased or decreased."

"I don't get how the energy density 'conservation' equation has to do with fluid pressure."

"Why does the buoyant force push objects upward no matter the shape? and I dont understand how to find the weight of displaced fluid."

"I did not quite understand the relationship of of the submerged volume and the volume of the object."

"I would just love to see some examples with numbers--buoyancy and energy density 'conservation' in particular."

I just need some specific examples of the equations to be gone over in class."

"I find it confusing when it comes to solving for a missing variable."

"I found nothing confusing."

What is the numerical value for atmospheric pressure (P_atm, at sea level), in units of Pa?

"1.013×10⁵ Pa."

"101,325 Pa."

"101.3 kPa."

"14.70?"

To three significant digits, what is the numerical value for the density of water, in units of kg/m³?

"1,000 kg/m³."

"1.000×10³ kg/m³."

"1 g/cm³ = 1.00×10³ kg/m³."

".001?"

To two significant digits, what is the numerical value for the density of air (at 20° C), in units of kg/m³?

"1.2 kg/m³."

"1.2041 kg/m³."

"9.98×10³ kg/m³?"

"I have no idea."

"I'm not really sure how to do this."

For the air pressure surrounding the balloon as it rises from ground level to the upper atmosphere, indicate the changes in each of the energy density forms of the atmosphere.
(Only correct responses shown.)

ρ_air·g·∆y: increases [45%]
∆P: decreases [54%]

For the water pressure that surrounded these cups as they were taken deep underwater, indicate the changes in each of the energy density forms of the water.
(Only correct responses shown.)

ρ_water·g·∆y: decreases [27%]
∆P: increases [64%]

For the submerged diver floating underwater, Newton's __________ law applies, and the (downwards) weight force and (upwards) buoyant force on the diver are __________.

first; balanced.	******************************* [31]
second; unbalanced.	********* [9]
(Unsure/lost/guessing/help!)	**** [4]

For the red ship (barely) afloat, Newton's __________ law applies, and its (downwards) weight force, the (downwards) oil platform's weight force, and the (upwards) buoyant force on the red ship are __________.

first; balanced.	************************ [24]
second; unbalanced.	**************** [16]
(Unsure/lost/guessing/help!)	**** [4]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"If ρ·g·∆y increases, does ∆P have to increase as well?" (No, an increase in one term must be balanced by a decrease in the other term. If ρ·g·∆y increases (say, from going higher up in the atmosphere), then ∆P must decrease, resulting in a lower pressure ("thin air") at that higher elevation.)

"Is energy density used when talking about the pressure in a tank with gases?" (Yes, if you "pressurize" the air in a tank, then you are doing work squeezing the air inside (either by putting more air in, reducing the volume inside, or heating up the contents), such that the energy per volume (i.e., pressure) would increase.)

"Can you explain how this makes sense: N/m² = (N·m)/(m³) = J/m³? I don't see it mathematically." (You're multiplying N/m² with m both on the top and bottom (this is allowed). A N·m is a joule, so you'll get joules per cubic meter. This is the justification for saying pressure (Pa, or N/m²) is equivalent to energy density J/m³.)

"Can we do more examples with numbers please?"

"I am confused with buoyant force."

"I don't understand the notation of the equations."

"The last two buoyancy questions I am assuming are not moving?" (Yes, that is implied from the word "floating.")

"Can Newton's second law be applied in the last problem if the ship is not moving?" (#wut)

"I am confused about the application of Newton's laws and the buoyant force here in the homework. Can we go over that as well as the other stuff mentioned earlier?"

"If you had an elephant-sized black hole, how many elephants would it weigh?" (Most likely more than one elephant. You could also throw a lot of elephants in there.)

Physics quiz archive: energy conservation, momentum conservation

Physics 205A Quiz 4, fall semester 2016
Cuesta College, San Luis Obispo, CA
Sections 70854, 70855, 73320, version 1
Exam code: quiz04th1R



Sections 70854, 70855, 73320 results

0- 6 :
7-12 :	**** [low = 9]
13-18 :	****************
19-24 :	*********************** [mean = 20.5 +/- 4.8]
25-30 :	******** [high = 27]

Online reading assignment: fusion, nebulae, star cluster ages (NC campus)

Astronomy 210, fall semester 2016
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on fusion, nebulae, and star cluster ages.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"Fusion energy is really exciting, if we can start using it efficiently on Earth."

"Stars in stars clusters being born in the same time yet some stars age faster than others. I would assume they would age alike."

"The nebulas. Each having their own color and material was something new to me."

"I really enjoyed reading about the nebula clouds and am enjoyed learning what makes them beautiful colors."

"How stars form from the gaseous nebula clouds. Because it is so cool (or maybe hot) to see how something as large and hot as a star forms in somewhere as cold as space."

"I find your house party analogy actually really interesting and helpful. It adds a lot of humor to the lecture."

"How we get to talk about cheerleaders!"

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"H-R diagram--unsure how to properly interpret it."

"The technicality of how the nebula's form as well as cold fusion."

"I am having a hard time understanding why there is no mass/luminosity correlation for non main sequence stars."

"Confused on fusion rates compared to different stars."

"I found the colors of the nebulae confusing."

"Not much is confusing."

Rank the luminosities of these main-sequence stars (1 = brightest, 3 = dimmest). (There are no ties.)
(Only correct responses shown.)

Massive: brightest luminosity [94%]
Medium-mass (sunlike): medium luminosity [82%]
Low mass (red dwarf): dimmest luminosity [82%]

Rank the fusion rates of these main-sequence stars (1 = fastest, 3 = slowest). (There are no ties.)
(Only correct responses shown.)

Massive: fastest fusion rate [88%]
Medium-mass (sunlike): medium fusion rate [82%]
Low mass (red dwarf): slowest fusion rate [94%]

Fusion requires high temperatures in order for nuclei to move quickly enough to:

break heavy elements apart.	* [1]
create convection currents.	** [2]
overcome gravity.	* [1]
overcome repulsion.	********* [9]
(Unsure/guessing/lost/help!)	**** [4]

Briefly explain why "cold fusion" (producing energy from hydrogen fusion at room temperature) would be implausible.

"Because there must be enough heat for the molecules to overcome the Coulomb barrier (the fact that two positive charged nuclei repel each other), and collide with each other."

"It's impossible since the atoms wouldn't move fast enough to produce enough energy and would not overcome repulsion."

"Fusion requires heat, therefore 'cold fusion' wouldn't ever work."

"I can not at this moment."

Match the three different types of nebulae with their colors.
(Only correct responses shown.)

Emission: pink [65%]
Reflection: blue [77%]
Dark: brown/black [82%]

Match the three different types of nebulae with their composition.
(Only correct responses shown.)

Emission: hydrogen [88%]
Reflection: small dust particles [88%]
Dark: large dust particles [77%]

Rank the lifetimes of these main-sequence stars (1 = shortest, 3 = longest). (There are no ties.)
(Only correct responses shown.)

Massive: shortest main-sequence lifetime [65%]
Medium-mass (sunlike): medium main-sequence lifetime [88%]
Low mass (red dwarf): longest main-sequence lifetime [71%]

If there was an open invitation to a house party (no specific time given), when would you show up?

Early, or on time.	***** [5]
When the most people should be there.	*********** [11]
After most everyone has left.	* [1]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Will stars and nebulae eventually use up all the interstellar medium?" (Yes, but the accelerating expansion of the universe would probably overcome the tendency for interstellar gas and dust to gather together.)

"Is fusion the energy source for all stars or just the sun?" (Hydrogen fusion is the energy source for all main-sequence stars, including our sun. After the hydrogen is used up, then the star will begin to die as it attempts to restart fusion with heavier elements to provide energy.)

"Is there going to be an astronomy house party?" (#smh)

"I can bring chips."