
Look at these stars. Just look at them. And let's sort them by their brightnesses. But just their brightnesses, as we're going to ignore the colors of these stars (even though they do have different colors), and we're going to ignore the sizes of these stars as well (even though they do have different sizes). This is why the stars are represented here as squares that correspond to their relative brightnesses.

In this presentation we will discuss how star brightnesses are measured, and how we can determine whether a bright star or a dim star seen in the night sky is really bright or dim (or perhaps not really bright
or dim).

Star brightnesses are measured using a magnitude scale, with +1 for bright stars, and +6 for the dim stars. If the smaller positive number for brighter stars bothers you, think of ranking schemes (as did the ancient Greeks in originally setting up this scale), where the brightest stars are "first place" or "top tier" stars, and the dimmest stars are in "sixth place" or "bottom tier" stars. And the scale did need to get revised, as there a few stars that blow the top off the original +1 to +6 scale. Brighter than the "first place" +1 stars are "zero place" stars, and brighter than those stars are "–1 place" stars. These are the very bright stars, and the scale has larger negative numbers for progressively brighter stars. There are also lots of stars dimmer than +6, and the scale has larger positive numbers for progressively dimmer stars.
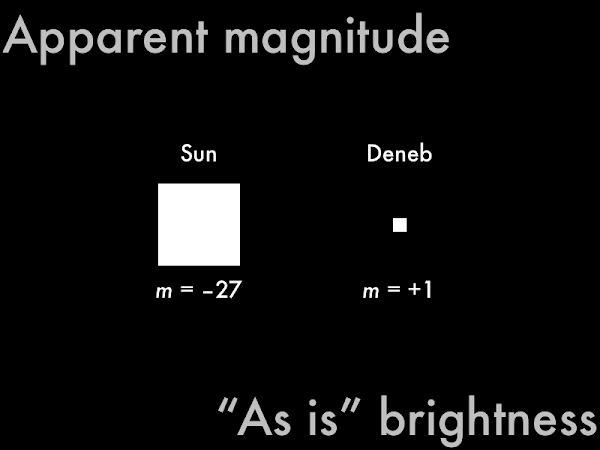
The apparent magnitude
m (lower case italics "m") of a star is the "as is" brightness as seen by an observer on Earth, without compensating for distance. The sun is not the brightest star ever, but being extremely close makes it
seem brighter than all other stars. Deneb is one of the brightest stars ever, but being extremely far away makes it
seem dimmer than many other stars. So, apparent magnitude is not really a fair way to compare the brightnesses of stars, as some stars cheat (like our sun), and some stars get dissed (like Deneb).

In order to compensate for the effect of distances on star brightnesses, we need to be able to measure their distances. This is done using parallax, which is the shift in perspective as you look at an object from two different viewpoints, such as Diane Lane's left eye and right eye in
Under the Tuscan Sun (Blue Gardenia Productions/Buena Vista Pictures, 2003).
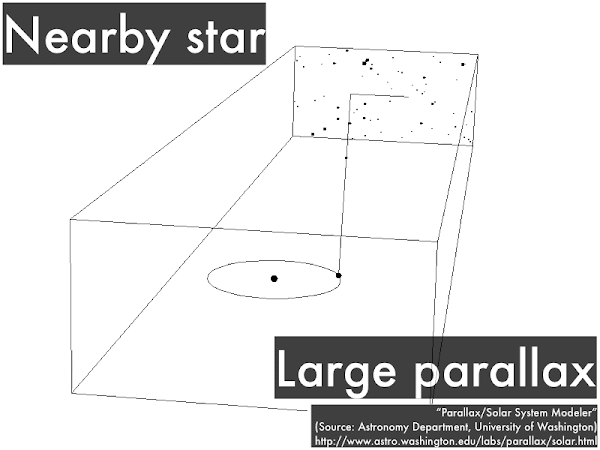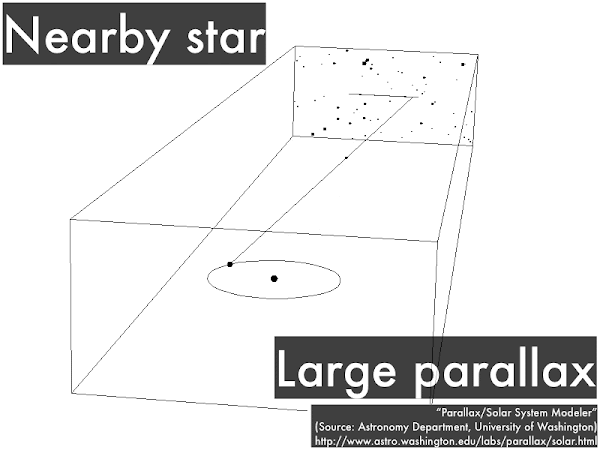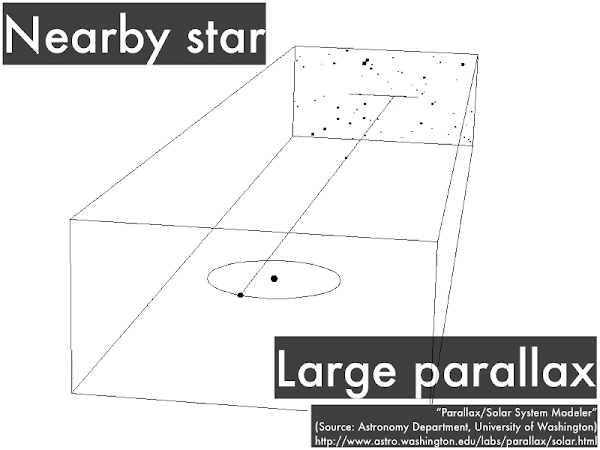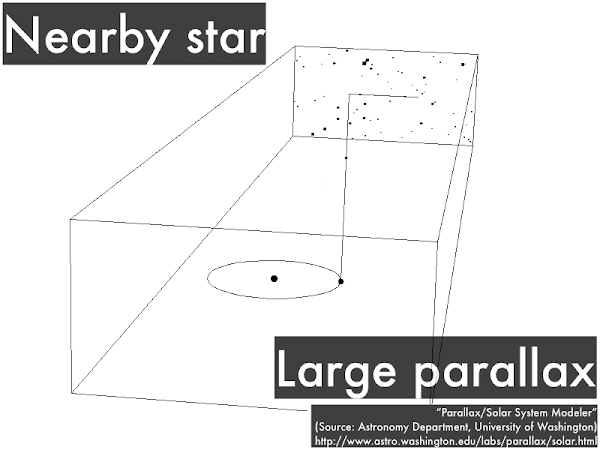
In astronomy the two different viewpoints for looking at a star is from Earth when it is at one end of its orbit, then six months later from Earth when it is at the other end of its orbit. In this case the nearby star will appear to shift back and forth, and the amount of this shift (its parallax) can be related to its distance.
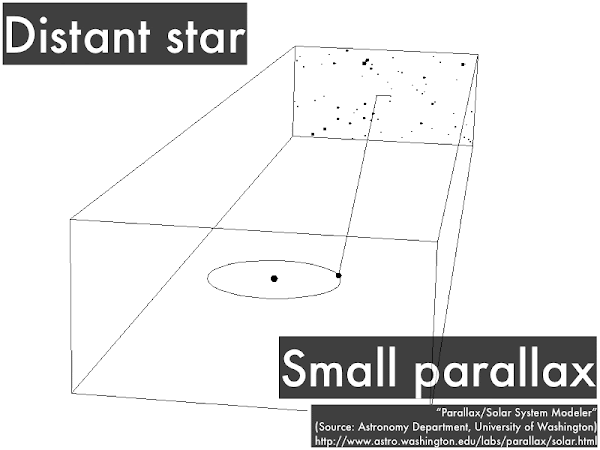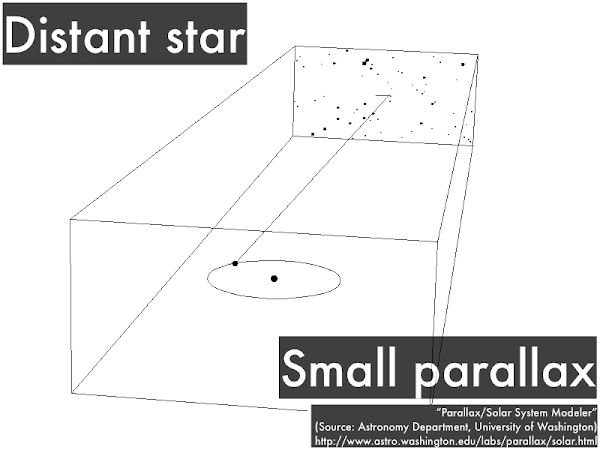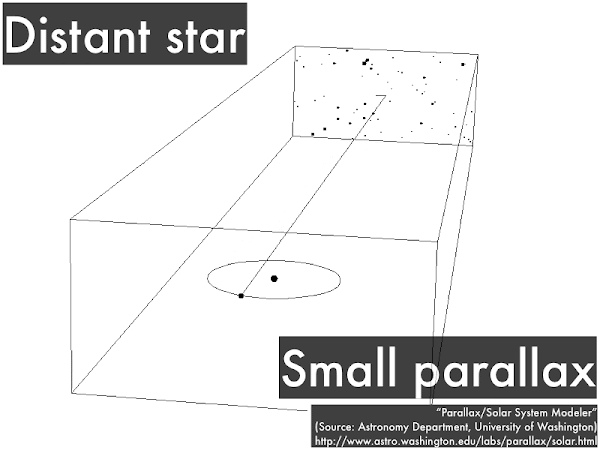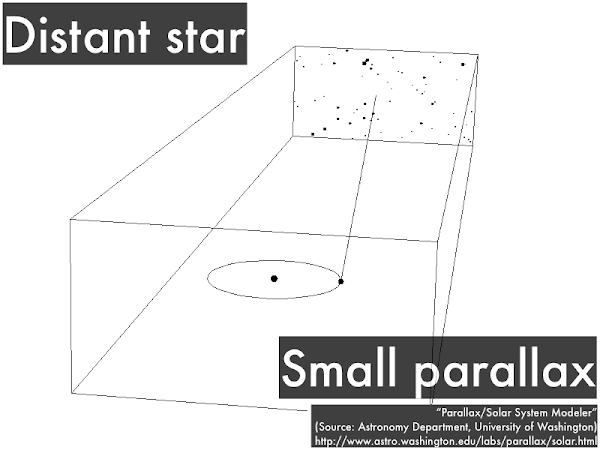
Again we look at a star from Earth when it is at one end of its orbit, then six months later from Earth when it is at the other end of its orbit, but this time the star is farther away. In this case the distant star will appear to shift back and forth a smaller amount, and the smaller amount of this shift (a smaller parallax) can be related to a greater distance. In practice, this shift is an angle measured not in degrees, but in very small units of arc seconds (where 1 arc second is 1/3,600th of a degree), and a star that shifts by 1 arcsecond corresponds to being at a distance of 1 parsec away ("a parallax angle of 1 arc second"), or 3.26 light years away. Parallax shifts bigger than 1 arc second would correspond to stars closer than 1 parsec away, while parallax shifts smaller than 1 arc second would correspond to stars farther than 1 parsec away.

Now that we have one method (actually several other methods are also used) to determine how close or how far away a star is, we can then determine the actual brightness of a star by compensating for its distance. In the case of the sun, we know that it is extremely close, and if we conceptually push it back to an arbitrary "fair comparison distance" of 10 parsecs away, it will get dimmer.

Similarly for Deneb, we know that it is extremely far away, and if we conceptually bring to closer to the arbitrary "fair comparison distance" of 10 parsecs away (just like we did for the sun), it will get brighter.

And now that we have compensated for the extreme closeness of the sun and the extreme distance of Deneb by
conceptually relocating them to the same "fair comparison distance" of 10 parsecs away, we can see that the sun is actually much dimmer than Deneb. The brightnesses of stars when placed 10 parsecs away is their absolute magnitude
M (actually, upper-case cursive "M"), and if we conceptually relocate every other star to 10 parsecs (once we know their actual distances), absolute magnitude becomes a way to compare the "actual" brightnesses of stars with each other, something that will be important in the
next presentation on star temperatures and sizes.
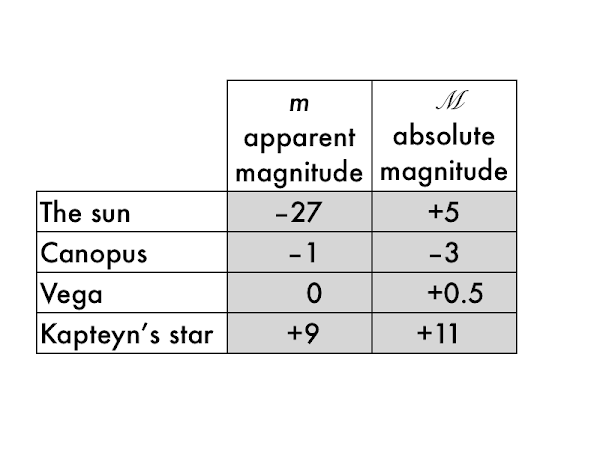
Let's practice applying these concepts to some stars.
Rank these stars from brightest to dimmest, as seen from Earth:
______, _____, _____, _____.
Rank these stars from brightest to dimmest, if relocated to 10 parsecs from Earth.
______, _____, _____, _____.
List the star(s) (if any) that get dimmer when relocated from their original positions to 10 parsecs from Earth (these are the stars that are located nearer than 10 parsecs from Earth).
______, _____, _____, _____.
List the star(s) (if any) that get brighter when relocated from their original positions to 10 parsecs from Earth (these are the stars that are located farther than 10 parsecs from Earth).
______, _____, _____, _____.











No comments:
Post a Comment