 Other than the sun, how do we know the sizes of other stars, which are so far away, that they essentially appear to be mere points of light?
Other than the sun, how do we know the sizes of other stars, which are so far away, that they essentially appear to be mere points of light? In order to answer the question of star size, we will need to look at two other properties of stars--the first being luminosity, which (as previously discussed last week) is related to absolute magnitude, which are measures of the intrinsic brightness of stars, once you take into account how close or far away they are.
In order to answer the question of star size, we will need to look at two other properties of stars--the first being luminosity, which (as previously discussed last week) is related to absolute magnitude, which are measures of the intrinsic brightness of stars, once you take into account how close or far away they are. The other related star property is color. Next time you are in a fairly dark sky, take a look at the colors of the stars--while many are white, some stars have a few select colors. Together the luminosity and the color of a star can be used to indirectly deduce its size.
The other related star property is color. Next time you are in a fairly dark sky, take a look at the colors of the stars--while many are white, some stars have a few select colors. Together the luminosity and the color of a star can be used to indirectly deduce its size. The process of finding the size of a star from its luminosity and color involves some math skills, but not to worry, as this presentation will take through a method of "doing math without doing math" (but if you are more comfortable tackling the algebra, then by all means do so). Technically stars can be described as blackbodies, as they are hot, dense sources of light, as discussed in a previous presentation.
The process of finding the size of a star from its luminosity and color involves some math skills, but not to worry, as this presentation will take through a method of "doing math without doing math" (but if you are more comfortable tackling the algebra, then by all means do so). Technically stars can be described as blackbodies, as they are hot, dense sources of light, as discussed in a previous presentation. First, Wien's law, which relates the color of a star to its temperature.
First, Wien's law, which relates the color of a star to its temperature.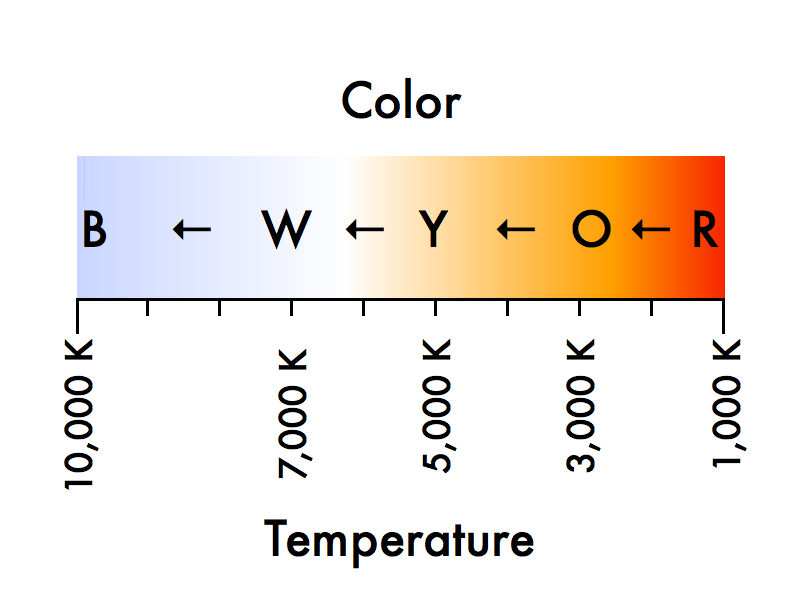 The coolest visible stars will appear red, but warmer and warmer stars will appear orange, then yellow like our sun, and stars hotter than the sun will appear white-hot, then blue-hot. (Stars cooler than this range will primarily give off infrared light, while cannot be seen; while stars much hotter than this range will primarily give off ultraviolet light, but still appear blue to our eyes.)
The coolest visible stars will appear red, but warmer and warmer stars will appear orange, then yellow like our sun, and stars hotter than the sun will appear white-hot, then blue-hot. (Stars cooler than this range will primarily give off infrared light, while cannot be seen; while stars much hotter than this range will primarily give off ultraviolet light, but still appear blue to our eyes.) These are not all the colors of the rainbow--what's up with that? But the important point is that you know the relative temperature of a star just by observing its color. Looking at the stars at night, can you point out the hot stars? The not-so-hot stars?
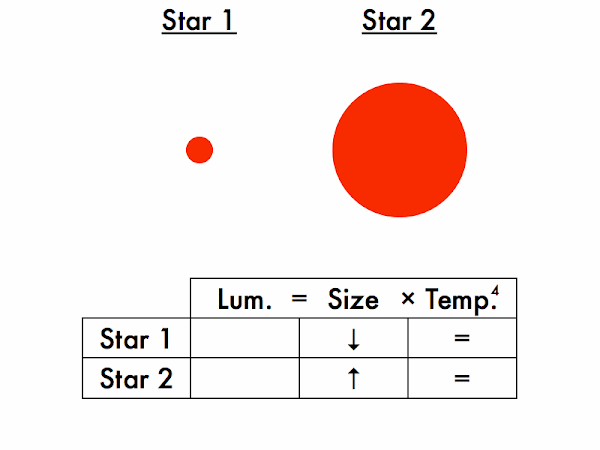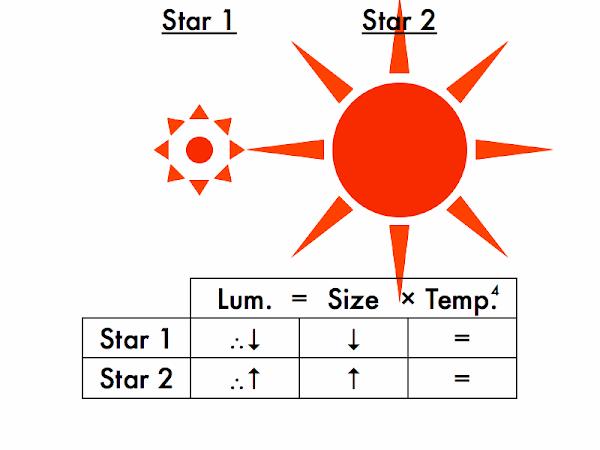
 Second, the Stefan-Boltzmann law, which relates the luminosity, size, and temperature of a star.
Second, the Stefan-Boltzmann law, which relates the luminosity, size, and temperature of a star.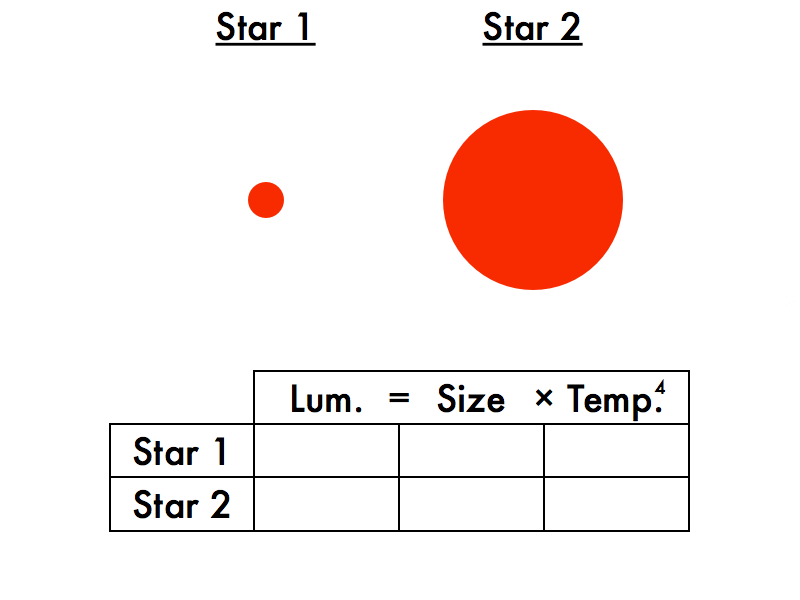 Let's compare two stars at a time. We'll be filling in entries in this box, which will you practice further in the subsequent in-class activity.
Let's compare two stars at a time. We'll be filling in entries in this box, which will you practice further in the subsequent in-class activity. 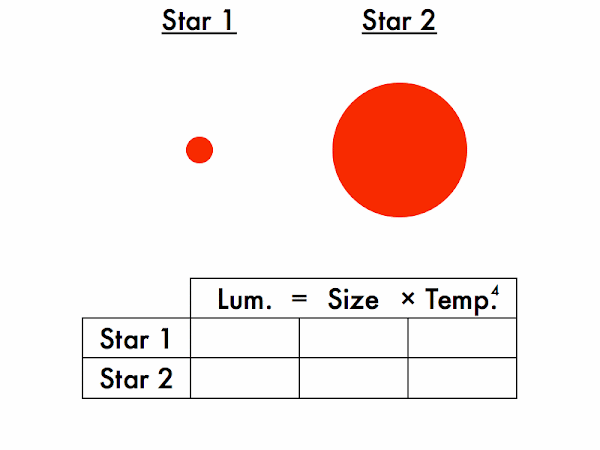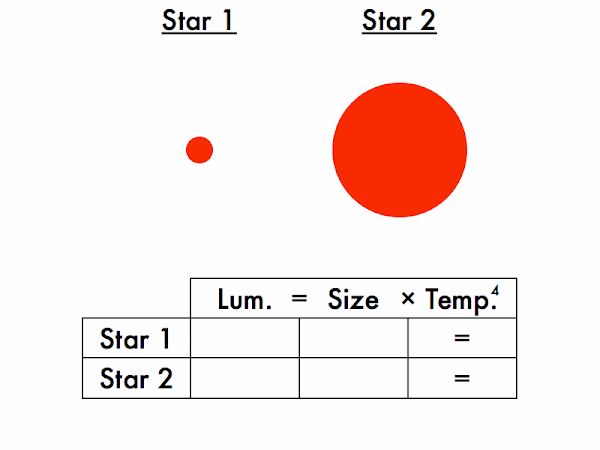
Which star is larger, and which is smaller? (They're meant to be the same size, but may appear slightly different in size due to an optical color illusion.)
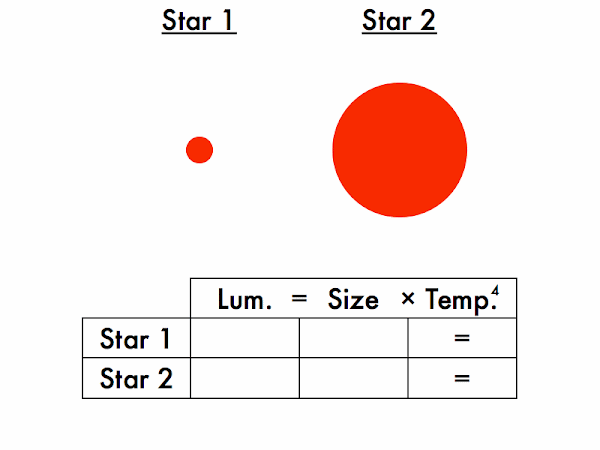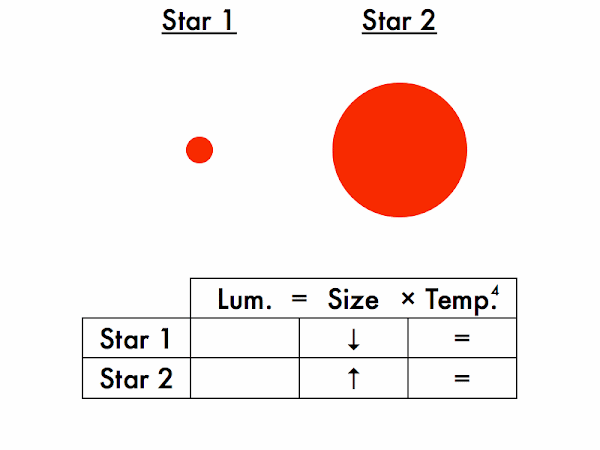
Which star is more luminous, and which is less luminous? How do you know this? (For the Stefan-Boltzmann law to be satisfied on both sides of these equations, given two stars of the same size, the hotter star must be more luminous, and the cooler star must be less luminous.)
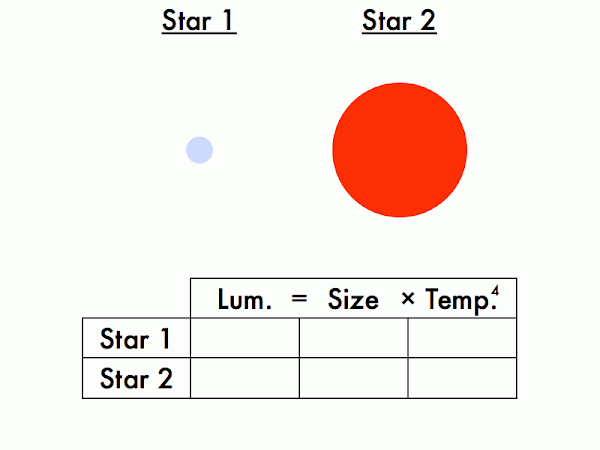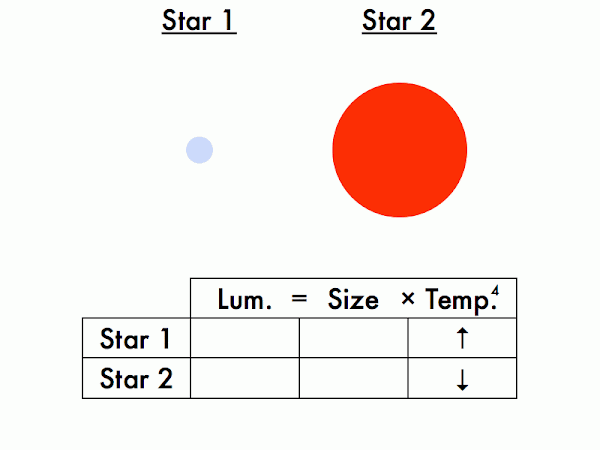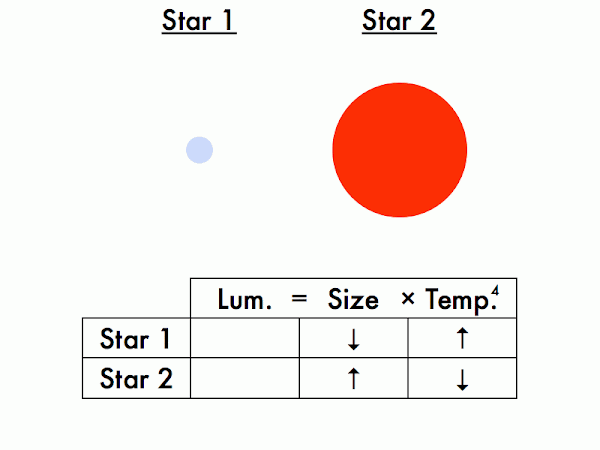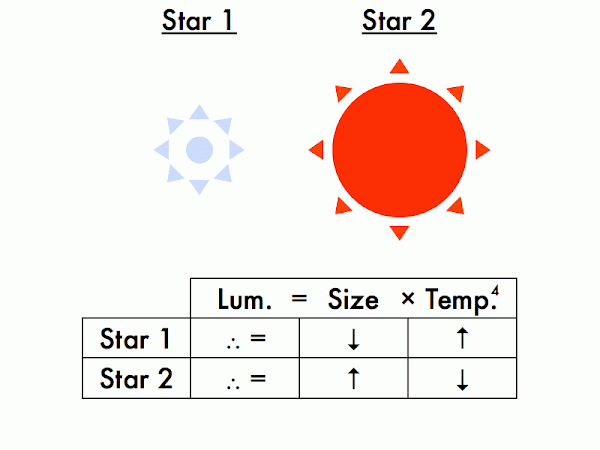
Which star is larger, and which is smaller? (Okay, this should be obvious.)
 Third, determining star sizes.
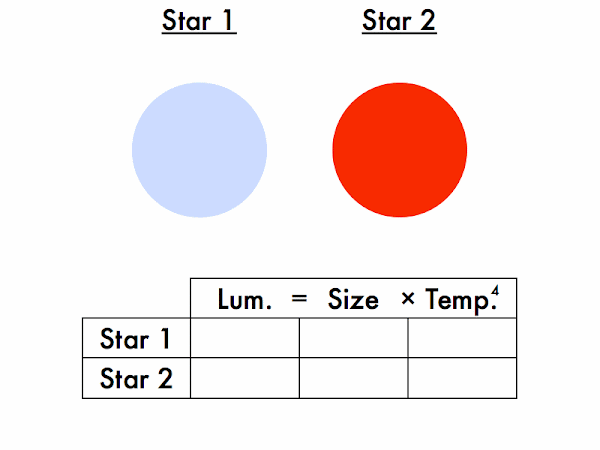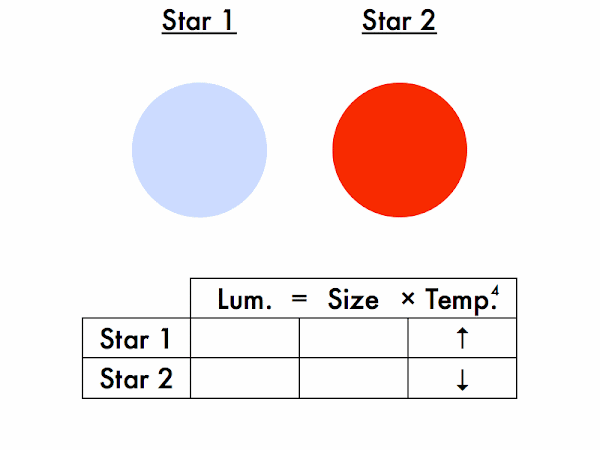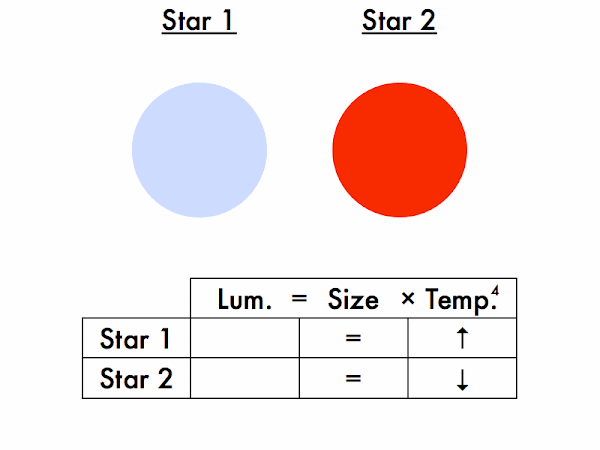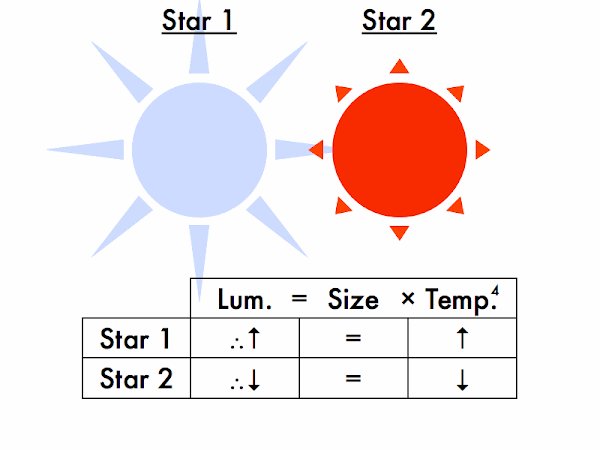
Third, determining star sizes. This is a summary of Wien's law, and the Stefan-Boltzmann law. We can directly observe the color of star, so can determine its temperature.
This is a summary of Wien's law, and the Stefan-Boltzmann law. We can directly observe the color of star, so can determine its temperature.Also we can figure out the luminosity of a star--a measure of its "true" brightness--by taking into account its distance. So once temperature and luminosity are known, then we can determine the size of star!
 Think about that when you contemplate the night sky, with stars of different luminosities, and different colors...
Think about that when you contemplate the night sky, with stars of different luminosities, and different colors... ...and using math (or our comparative box-entry method) to determine the sizes of stars, which can vary immensely, and not even the extremely small and extremely large stars can be shown here to the same scale as these stars.
...and using math (or our comparative box-entry method) to determine the sizes of stars, which can vary immensely, and not even the extremely small and extremely large stars can be shown here to the same scale as these stars.In the subsequent in-class activity you will be working in groups to determine the relative sizes of select pairs of stars given the luminosities and temperatures using the comparative box-entry method. Make sure you understand this application of Wien's law and the Stefan-Boltzmann law enough to be able to explain your reasoning on an exam essay question!
No comments:
Post a Comment