Cuesta College, San Luis Obispo, CA
Students have a bi-weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.
The following questions were asked on reading textbook chapters and previewing a presentation on ideal fluid flow.

Selected/edited responses are given below.
Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.
"This section was mostly about flow rates the the motion of fluids. Since most fluids are incompresiable, they can be used in the equation of continuity because the mass flow rate is equal throught a tube. Bernoulli's equation links fluids and energy together."
"The difference between compressible/incompressible fluids. That water flow can be either laminar or turbulent."
"We are now going over fluid in motion. When water is going through a pipe at a certain speed it exits the pipe at that same rate and volume. If the water is flowing from a narrow opening to a larger opening, then the water will go from a faster speed to a slower speed as it flows from one area to the next. And the same for the other way around."
"How the flow of ideal fluid works and how it relates to volume and speed and whatnot. The more fluid crammed into a smaller area yields increased velocity."
"I understood from the blog was the description of ideal fluids. Ideal fluids are incompressible, laminar, and non-viscous."
"Steady flow is when a fluid has the same velocity from one point to the other, but it can still be steady while the velocity changes after that point if it still is constant. I understand that 'ρ' = fluid density, 'A' = cross-sectional area of tube, and 'v' = fluid speed."
"Ideal fluids are not compressible and also have a laminar flow, where the particles flow together side by side making for an easy movement, and should also have a non-viscous flow. With a changing radius of a tube holding water, the volume of the water does not change, however if the radius of a tube increases, then the speed will decrease."
"I understand the concept of increasing area means decreasing speed and vice versa when it comes to flowing fluids. This is easy for me because I learned it in physiology with blood flowing in blood vessels."
Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.
"Knowing how to whether/if cross-sectional area and speed is constant at a time and place."
"Volume flow conservation is confusing, in how it works with volume and time."
"Does pressure increase as the radius of a pipe pumping water decreases?"
"I would like to go over Bernoulli's equation and some problems to practice its application. Some of the terms in it were a bit confusing to follow. I feel good about the concept of how fluid flows through a pipe, but it is confusing when it starts being put in the equation."
"The second conservation law (Bernoulli's equation) for ideal fluids is somewhat confusing to me. The equation seems pretty difficult for me."
"I was confused with Bernoulli's conservation equation. I'm confused on how to relate static fluids with ideal fluids."
"Not sure how the gravitational potential energy density term is involved in ideal fluids."
"I thought pressure within the system should not change?"
"I'm not really sure when you use the volume flow conservation equation."
"The last few questions putting all of the terms together in Bernoulli's equation confused me. I don't understand the changes in pressure in connection with the area and speed changes."
"Just number examples, homie."
"I found nothing confusing."
What is the SI (Système International) unit for volume flow rate?
"Meters cubed per second."
"m3/s."
"Cubic meters per second."
"m3/s = Pascals?"
"J/m3?"
"kg/s?"
"The SI unit for volume flow rate is inches and yards?"
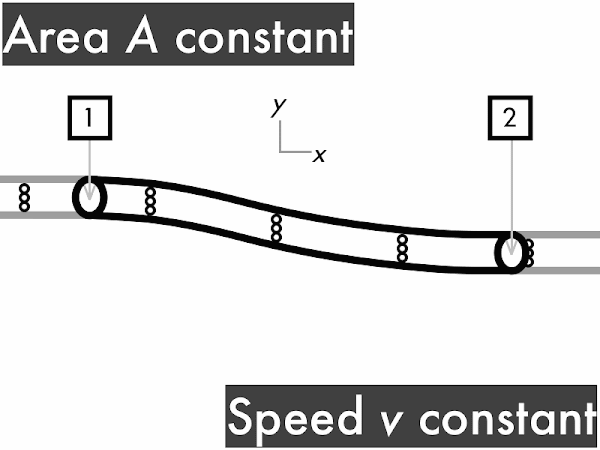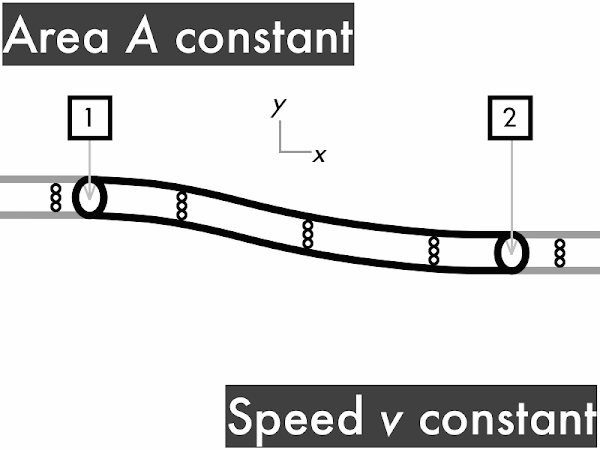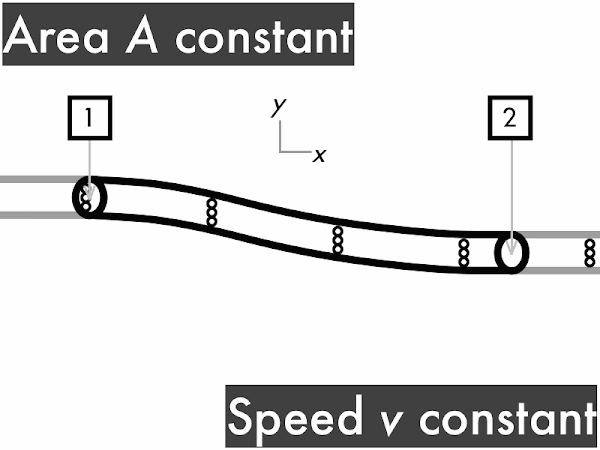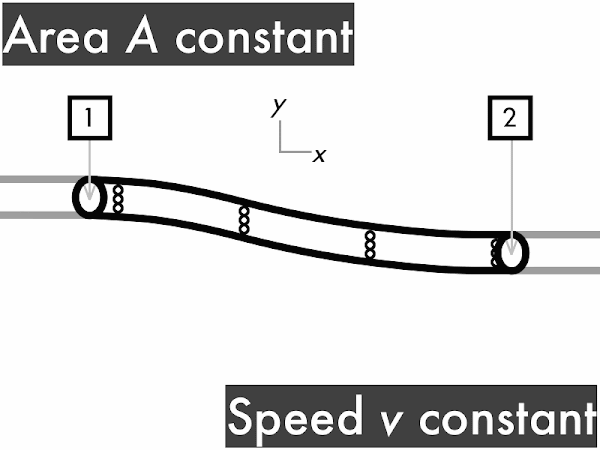
decreases. * [1] remains constant. ***************************************** [41] increases. [0] (Unsure/lost/guessing/help!) * [1]

decreases. *********************** [23] remains constant. ********* [9] increases. ******** [8] (Unsure/lost/guessing/help!) *** [3]
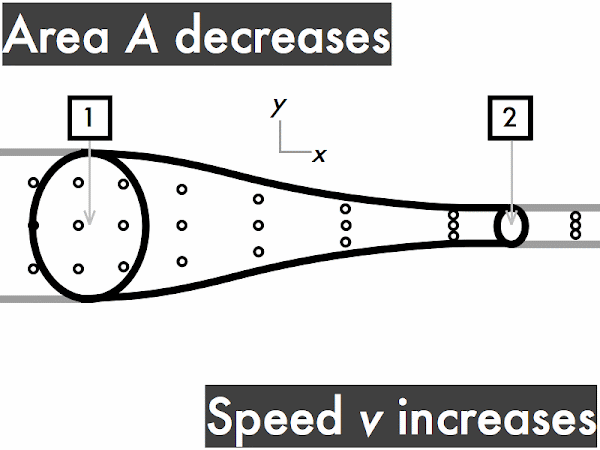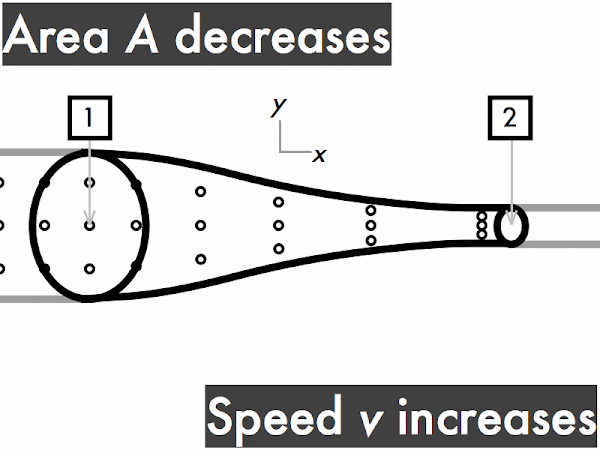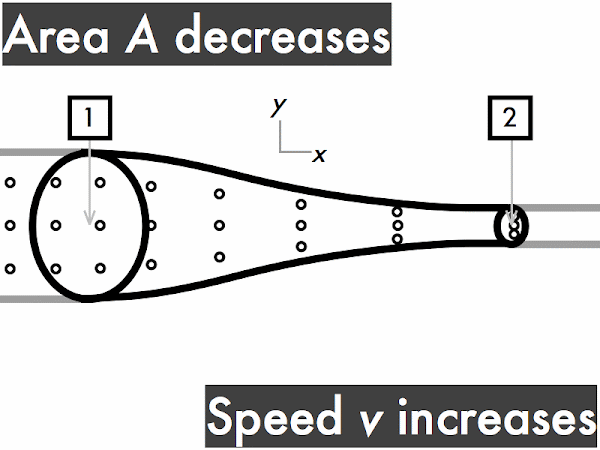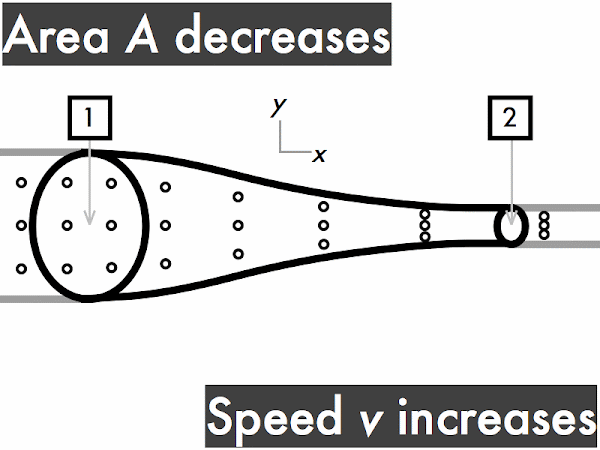
decreases. ********* [9] remains constant. ********** [10] increases. ********************** [22] (Unsure/lost/guessing/help!) ** [2]
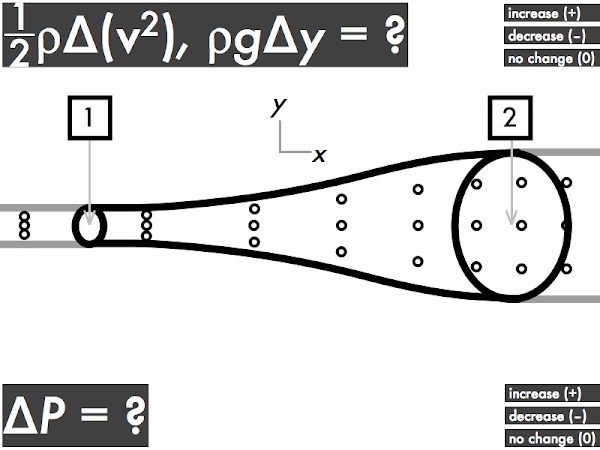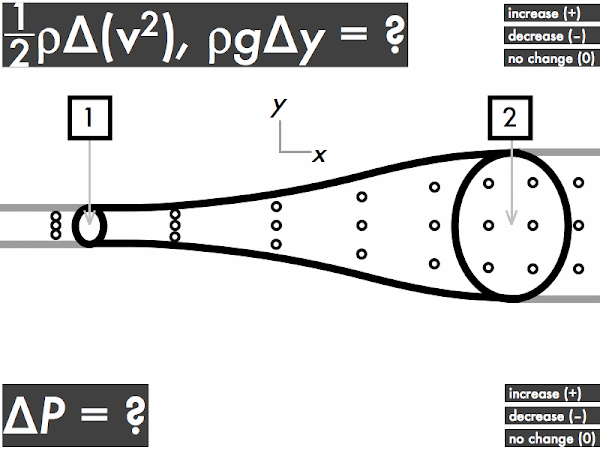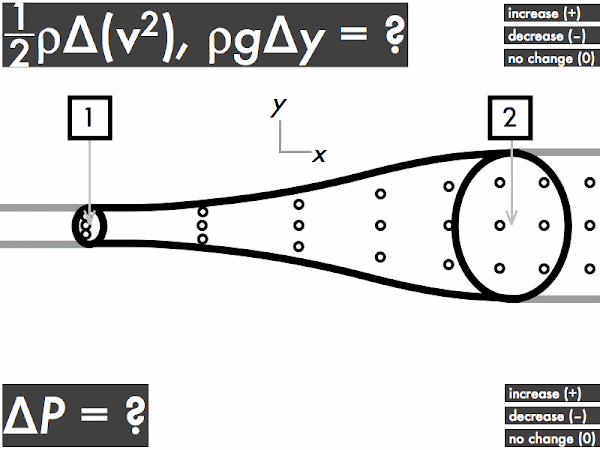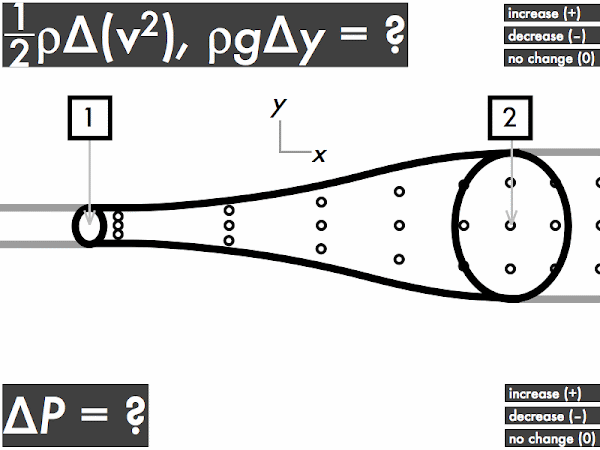
(Only correct responses shown.)
(1/2)·ρ·∆(v2): decreases [40%]
ρ·g·∆y: no change [33%]
∆P: increases [21%]

(Only correct responses shown.)
(1/2)·ρ·∆(v2): increases [42%]
ρ·g·∆y: no change [30%]
∆P: decreases [56%]

(Only correct responses shown.)
(1/2)·ρ·∆(v2): no change [70%]
ρ·g·∆y: decreases [12%]
∆P: increases [7%]
Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.
"Isn't water at the bottom of the ocean more compressed that water on the surface would that make it technically compressible?" (Yes, according to the European Space Agency, the increase in water density is approximately 4% in the deepest parts of the ocean (the Marianas Trench), but since most of our calculations only have two significant figures, then for our purposes water can be considered incompressible.)
"How should we be keeping track of all these equations, in these last few weeks we have gotten like 10 new ones?" (At the bottom of the practice quizzes (also on the last page of the worksheet packets), label each variable, and summarize each equation. This is the vocabulary and language of physics, so it will take some time to become fluent, by using these equations in the homework.)
"Can we go over the water flowing through widening and narrowing cross-sectional areas and ascending/descending pipes?" (Yes. But thanks for trying--sometimes I don't realize how difficult things are going to be until I make you try them out.)
"How does the ∆y term figure into the conservation equations for ideal fluid flow?" (For static fluids, a decrease in height (making ∆y negative) corresponded to an increase in pressure (making ∆P positive). For ideally flowing fluids, the increase or decrease in ∆y must be tied to both changes in pressure (∆P) and changes in kinetic energy density ((1/2)·ρ·(∆v2). This is essentially like using the transfer-balance energy conservation equation with no non-conservative work (making the left-hand side of the equation zero), and three (or more) energy change terms on the right-hand side.)
"So when cross-sectional area decreases, it increases the speed and pressure of the fluid?" (Assuming that the pipe is horizontal, yes, the speed increases, but there must be a corresponding decrease in pressure. We'll cover this in more detail in class.)
"How can I pass this class?" (See me during office hours. We'll go through your individual case and break it down for you.)
"No questions."
"No comment."
"Uhh."
No comments:
Post a Comment