Physics quiz question: block stopped by compressing spring

Physics 205A Quiz 4, fall semester 2009
Cuesta College, San Luis Obispo, CA

Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Problem 6.58, Comprehensive Problem 6.82

An 0.080 kg block traveling horizontally at 5.5 m/s hits a horizontal spring (k = 320 N/m) that is initially uncompressed. Neglect friction and drag. As a result the block is brought to a rest when the spring is compressed by:
(A) 0.037 m.
(B) 0.061 m.
(C) 0.087 m.
(D) 1.2 m.

Correct answer (highlight to unhide): (C)

Starting with the energy balance equation:

W_nc = ∆KE_tr + ∆PE_grav + ∆PE_elas,

where W_nc = 0 (no external gains/losses of mechanical energy), and ∆PE_grav = 0 (as there is no change in elevation of the block as it travels horizontally to come to rest), such that:

0 = ∆KE_tr + ∆PE_elas,

0 = (1/2)·m·∆(v²) + (1/2)·k·∆(x²),

0 = (1/2)·m·(v_f² – v₀²) + (1/2)·k·(x_f² – x₀²).

With initial parameters of v₀ = +5.5 m/s (block is moving) and x₀ = 0 (spring is relaxed/uncompressed), and final parameters v_f = 0 (block at rest), then the distance x_f that the spring has been compressed from equilibrium can now be solved for:

0 = (1/2)·m·(0² – v₀²) + (1/2)·k·(x_f² – 0²),

0 = –(1/2)·m·v₀² + (1/2)·k·x_f²,

k·x_f² = m·v₀²,

x_f = v₀·(m/k)^1/2,

x_f = (5.5 m/s)·((0.080 kg)/(320 N/m))^1/2 = 0.08696263565 m,

or to two significant figures, the spring is compressed by 0.087 m.

(Response (A) is (m·v₀/k)^1/2; response (B) is v₀·(m/(2·k))^1/2; response (D) is v₀·(2·g)^1/2.)

Sections 70854, 70855
Exam code: quiz04s7aT
(A) : 12 students
(B) : 16 students
(C) : 17 students
(D) : 3 students

Success level: 35%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.37

Physics quiz archive: vectors, projectile motion, forces

Physics 205A Quiz 3, fall semester 2014
Cuesta College, San Luis Obispo, CA
Sections 70854, 70855, 73320, version 1
Exam code: quiz03fkfs



Sections 70854, 70855, 73320 results

0- 6 :	**** [low = 3]
7-12 :	*********
13-18 :	***************************** [mean = 18.4 +/- 6.1]
19-24 :	**********************
25-30 :	******** [high = 30]

Online reading assignment: quantum leaps, sun's outer layers (NC campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on quantum leaps, and the sun's outer layers.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"The granulated nature of the sun's surface was interesting because you'd think it was sort of smooth since it's a giant ball of flaming gas and also because the granulation reminds me a lot of what happens when you mix watercolor paint with sugar water (very cool, do recommend looking at it)."

"Sunspots are interesting because they are caused by magnetic fields."

"I found it interesting that sunspots are slightly cooler than the remaining surface of the sun. I thought the opposite would be true."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"How electrons move from level to level in an atom. I don't understand how they do this, and, more importantly, how does this cause light?"

"The concept of electrons jumping energy levels and giving off or taking electrons. This is confusing because I can't visualize it and make sense of it."

"Nothing was really confusing. It will just take a while to bring back all the chemistry terms."

"For sunspots I got confused on how there could be a non-circulating part of the surface of the sun. It was confusing because I do not understand how that is possible?"

An electron in an atom must emit a photon when it jumps from a __________ energy orbital to a __________ energy orbital.

lower; higher.	***** [5]
higher; lower.	************************** [26]
(Both of the above choices.)	[0]
(Unsure/guessing/lost/help!)	[0]

An electron in an atom must absorb a photon when it jumps from a __________ energy orbital to a __________ energy orbital.

lower; higher.	*************************** [27]
higher; lower.	**** [4]
(Both of the above choices.)	[0]
(Unsure/guessing/lost/help!)	[0]

The exterior of the sun, from inner to outermost layers, are the:
(Only correct responses shown.)

inner: photosphere [84%]
middle: chromosphere [77%]
outer: corona [81%]

State your preference regarding miso soup.

Strongly dislike.	* [1]
Dislike.	* [1]
Neutral.	** [2]
Like	************ [12]
Strongly like.	*********** [11]
(I don't know what miso soup is.)	**** [4]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"I just can't stand miso soup at all."

"Miso soup is pretty great, to be honest."

"The sun can be anything it wants! If it wants to be a TV with a magnet, or a lava lamp, then let it! Equality for the sun! We owe it that much! P. S. The sun wants us to have a miso soup party."

"I think P-dog looks a bit like Glenn from the Walking Dead TV series. The character is badass."

Online reading assignment: work and energy

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on work and energy.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"The faster an object moves, the more translational kinetic energy it will have. That was a pretty straightforward idea. It also made sense that when an object is stationary it has no translational kinetic energy."

"For something to do work on an object, that something would have to put that object in motion. Even though something is exerting force on an object, it is not classified as work unless there is an energy transfer onto the object."

"Translational kinetic energy is the energy of motion and it depends on mass and speed of an object. Work causes changes in this kinetic energy."

"Forces can do work in order to do work on or against an object. If the work is done on an object, then that means that the work is increasing the objects motion in the same direction. If the work is doing work against an object, then that means the work is decreasing the object's motion in the opposite direction."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I could use some explanation on the equation for work."

"I was a little confused about the relationship between work and translational kinetic energy. I don't understand why if the work is negative that the change in kinetic energy also has to be negative and vice versa."

"I don't quite understand the angles associated with zero work."

"The work-energy theorem--the relationships between kinetic energy and work are still cloudy in my mind.

Explain how the SI (Système International) unit for work is related to the SI unit for force.

"They both use newtons."

"They both can be expressed in joules."

"Work has the newton-meter unit, which is newtons times meters. Force has units of just newtons. Work is force, but takes into account displacement."

"Work uses joules, which is force multiplied by displacement."

Match the description of the work exerted by these forces for each object. (Only correct responses shown.)

Pushing in the same direction of motion: work done "on" the object (positive work). [80%]
Pushing opposite the direction of motion: work done "against" the object (negative work). [87%]
Pushing 90° sideways to the direction of motion: no work done. [58%]
Pulling such that the angle between the force and motion is an acute angle (between 0° and 90°): work done "on" the object (positive work). [63%]
Pulling such that the angle between the force and motion is an obtuse angle (between 90° and 180°): work done "against" the object (negative work). [63%]

For the catapulted squirrel, the bungee cord force does work __________ the squirrel, which __________ the squirrel's translational kinetic energy.

on; increases.	******************************************* [43]
against; decreases.	********* [9]
(Unsure/lost/guessing/help!)	******** [8]

For the braking car, the brakes do work __________ the car, which __________ the car's translational kinetic energy.

on; increases.	**** [4]
against; decreases.	************************************************** [50]
(Unsure/lost/guessing/help!)	****** [6]

For Mrs. P-dog being catapulted, the bungee cords do work __________ Mrs. P-dog, while the weight force does work __________ Mrs. P-dog.

on; on.	* [1]
on; against.	**************************************** [40]
against; on.	****** [6]
against; against.	**** [4]
(Unsure/lost/guessing/help!)	********* [9]

For Mrs. P-dog's translational kinetic energy to be increased while being catapulted, the amount of work from the bungee cords must be __________ the amount of work from the weight force.

less than.	* [1]
the same as.	***** [5]
greater than.	********************************************* [45]
(Not enough information is given.)	[0]
(Unsure/lost/guessing/help!)	********* [9]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Did that catapulted squirrel die? (I do not know the answer to that question. Sounds like some experimental data needs to be collected.)

"Why are we more concerned with the change in K_tr than how much K_tr an object has? (Ask the squirrel. Life is not really about how much translational kinetic energy you happen to have, it only gets interesting when your translational kinetic energy changes...suddenly.)

"I don't know what to put here." (You just did.)

"Is there a situation when work against goes against the direction of motion? Could we go over the angles of the work?" (Yes, and yes.)

"It seems like the work should always be positive; it seems like if the work amount is negative then it is essentially a waste of energy." (Exactly. But sometimes you have to slow down your car with your brakes.)

Astronomy current events question: computer simulations of interactive dark matter

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Durham University news release, "Interactive Dark Matter Could Explain Milky Way’s Missing Satellite Galaxies," (September 9, 2014)
https://www.dur.ac.uk/news/newsitem/?itemno=22041

By studying __________, scientists proposed that dark matter interactions could explain why the Milky Way is surrounded by very few satellite galaxies.
(A) captured dark matter particles.
(B) the cosmic background radiation.
(C) computer simulations.
(D) gravitational lensing.
(E) neutrinos given off by the sun.

Correct answer: (C)

Student responses
Sections 70178, 70186
(A) : 13 students
(B) : 5 students
(C) : 17 students
(D) : 2 students
(E) : 6 students

Astronomy current events question: Subaru Telescope adaptive optics system

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

John Bochanski, "Next-Gen Adaptive Optics," (September 9, 2014)
http://www.skyandtelescope.com/astronomy-news/next-gen-adaptive-optics-09092014/

The Subaru Telescope on Mauna Kea is testing a new adaptive optics system, where a computer rapidly changes the shape of the telescope mirror to correct for:
(A) Earth's rotation.
(B) local earthquakes.
(C) interstellar dust and gas.
(D) atmospheric turbulence.
(E) light pollution.

Correct answer: (D)

Student responses
Sections 70178, 70186
(A) : 3 students
(B) : 0 students
(C) : 3 students
(D) : 32 students
(E) : 5 students

Astronomy current events question: Europa plate tectonics

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Preston Dyches, Dwayne Brown, and Michael Buckley, "Scientists Find Evidence of 'Diving' Tectonic Plates on Europa," (September 8, 2014)
http://www.jpl.nasa.gov/news/news.php?release=2014-300

By mapping _________ on Jupiter's moon, Europa, scientists proposed its ice experiences plate tectonics similar to that on Earth.
(A) missing surface features.
(B) active ice volcanoes.
(C) moonquake zones.
(D) subsurface ocean currents.
(E) glacier flows.

Correct answer: (A)

Student responses
Sections 70178, 70186
(A) : 12 students
(B) : 10 students
(C) : 5 students
(D) : 5 students
(E) : 11 students

Online reading assignment: runaway planets, jovian planets, and dwarf planets (oh my!) (SLO campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on runaway planets (Venus and Mars), jovian planets (Jupiter, Saturn, Uranus and Neptune), and the dwarf planets (and the International Astronomy Union classification scheme).


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"How extremely harsh Venus' atmosphere is, mostly because how Venus is said to be supposedly similar to Earth (even though I understand why that is said)."

"I finally know why Pluto is not longer a planet due to its size and location."

"Venus is superhot and Mars is cold."

"The different landscapes of terrestrial planets."

"The outer planets of the solar system are called jovian planets because they resemble Jupiter."

"Jupiter's atmosphere. I can't even imagine what it would be like falling from the sky and not distinctly touching something (and know you're touching something different). You just drown on air that all of a sudden got thick."

"I didn't know Venus might have once had water."

"The reasoning why Pluto isn't a planet. I didn't know that a planet had to be large enough to dominate and gravitationally clear its orbital region of most or of all other objects."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"I don't understand why Jupiter has always been called a 'gas giant' when in fact it's mostly liquid."

"I thought all the greenhouse factors became confusing after I read all the different kinds there are for each planet."

"I don't clearly understand how Pluto doesn't meet the IAU criteria."

"Planet atmospheres. What makes others different from ours and how it got to be that way."

"I understood this sections more than other sections because it was just talking about the planets. Mostly just looking at the diagrams in the book confuse me."

Identify the relative amounts of these characteristics for Venus, compared to Earth. (Only correct responses shown.)

Volcanic outgassing, up until now: about the same as Earth [53%]
Heat from the sun: more than Earth [88%]
Amount of atmosphere, today: more than Earth [60%]
Interior core heat, today: about the same as Earth [40%]
Geologic activity, today: less than Earth [23%]

Identify the relative amounts of these characteristics for Mars, compared to Earth. (Only correct responses shown.)

Volcanic outgassing, up until now: less than Earth [68%]
Heat from the sun: less than Earth [80%]
Amount of atmosphere, today: less than Earth [83%]
Interior core heat, today: less than Earth [88%]
Geologic activity, today: less than Earth [68%]

Which jovian planet has the coolest interior temperatures?

Jupiter (most massive).	*** [3]
Saturn (most prominent rings).	**** [4]
Uranus (least active weather patterns).	***************** [17]
Neptune (farthest from the sun).	************** [14]
(Unsure/guessing/lost/help!)	** [2]

I believe Pluto should be a planet.

Strongly disagree.	**** [4]
Disagree.	******** [8]
Neutral.	************** [14]
Agree.	*********** [11]
Strongly Agree.	*** [3]

Briefly explain your answer to the previous question (whether Pluto should be a planet).

"It was originally said to be a planet for so long, I don't think it was okay for them to just change it."

"I solely base this on my terrible experience as a child of having a planet torn away from me."

"Although Pluto is a 'dwarf planet' it should still be considered a planet."

"Whether Pluto is a planet or not, does not effect my daily life so I'm indifferent."

"Pluto is not big enough to clear its own orbit."

"I was taught that Pluto was a planet, but there has to be rules to govern what is a planet and what isn't. So, in order to keep all of the new findings in order...there has to be order."

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Do you think Pluto should be a planet? And why do you hate Pluto?" (It's not personal--simply, life is just not supposed to be fair.)

Online reading assignment: uniform circular motion

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on uniform circular motion.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"Uniform circular motion will have velocity tangent to its circular path, and acceleration perpendicular to it, toward the center of the circle."

"How Newton's second law relates net force to circular motion. Even if the speed is constant, the direction is always changing."

"Nothing at all."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"The mathematical reasoning behind non-uniform circular motion is overly confusing. I find it difficult to translate this information into words."

"How to determine the direction of the net force for an object moving in a circle."

"While I understand most of the concepts, I don't get how to draw a free-body diagram for circular motion. And I don't understand what kind of questions you would ask about it."

For the "drifting" car (skidding around a circular track at constant speed), Newton's __________ law applies to its motion, and the forces acting on it add up to a net force that:

first; is zero.	* [1]
second; points to the left.	************************** [26]
second; points to the right.	************************** [26]
(Unsure/lost/guessing/help!)	***** [5]

At the moment when the woman is at the bottom of her swinging trajectory (when the rope is vertical), Newton's __________ law applies to her motion, and the forces acting on her add up to a net force that:

first; is zero.	************** [14]
second; points upwards.	************************* [25]
second; points downwards.	************* [13]
(Unsure/lost/guessing/help!)	****** [6]

At the moment when the motor scooter is on the left side of the screen (traveling out at you), Newton's __________ law applies to its motion, and the forces acting on it add up to a net force that:

first; is zero.	***** [5]
second; points to the left.	********************** [23]
second; points to the right.	************************* [25]
(Unsure/lost/guessing/help!)	****** [6]

At the moment when the car is at the very top of the loop-the-loop, Newton's __________ law applies to its motion, and the forces acting on it add up to a net force that:

first; is zero.	************* [13]
second; points upwards.	************* [13]
second; points downwards.	************************** [26]
(Unsure/lost/guessing/help!)	****** [26]

At the moment when a person is at the right edge of the screen (traveling out at you), Newton's __________ law applies to his/her motion, and the forces acting on him/her add up to a net force that:

first; is zero.	****** [6]
second; points to the left.	******************** [20]
second; points to the right.	******************** [20]
(Unsure/lost/guessing/help!)	************ [12]

At the moment when the car is at the very top of its mid-air trajectory, Newton's __________ law applies to its motion, and the forces acting on it add up to a net force that:

first; is zero.	*************** [15]
second; points upwards.	******** [8]
second; points downwards.	*************************** [27]
(Unsure/lost/guessing/help!)	******** [8]

At the moment when the skateboarder is at the very top of his mid-air trajectory, Newton's __________ law applies to his motion, and the forces acting on him add up to a net force that:

first; is zero.	************* [13]
second; points upwards.	********** [10]
second; points downwards.	*************************** [27]
(Unsure/lost/guessing/help!)	******** [8]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"I'm good on this section."

"I look forward to the help you will give us."

"These questions about the net force on all these objects are asked multiple times, but never actually explained. Can you draw diagrams for each of the examples? Going over what's different with these new scenarios, such as loops and vertical banks, would be very helpful!" (Yes. Looking over the class' responses for these questions, you'll need some time on this in class.)

"If an object in uniform circular motion has a constant speed, but a changing direction, does that mean that Newton's second law still applies?" (Yes, exactly because the direction part of its motion is changing.)

"Would circular motion ever have zero forces at the top of its trajectory?" (No.)

"Will sample questions/study guides be available similar to quiz questions to help us practice? I feel the problems from the textbook are very different from problems you give us in class, so this would be a lot of help." (Yes, before every quiz (and exam) you'll get to work on the previous year's quizzes (and exams) for review. The older quiz and exam questions that are done as examples in class are intended to be different than those from the textbook, in being more direct in testing your understanding of the concepts involved, as opposed to being able to blindly solve for something.)

Online reading assignment: runaway planets, jovian planets, and dwarf planets (oh my!) (NC campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on runaway planets (Venus and Mars), jovian planets (Jupiter, Saturn, Uranus and Neptune), and the dwarf planets (and the International Astronomy Union classification scheme).


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"It was cool that there are a lot of other Pluto-like objects on the outskirts of our solar system."

"The differences between Venus and Earth because of the distance between the sun to either planet and it's terrifying knowing that Earth could have been Venus' fate had it been closer."

"Other planets have volcanos and rocks. I know that is vague but I just thought they were round hard objects with plain surfaces."

"The criteria to whether or not an object is to considered a planet or not. I found this interesting because I had no idea why Pluto was 'discharged' of its title of a planet, but now I know that since it doesn't dominate its orbit it's not a planet."

"Venus' and Mars' greenhouse effects, and how each one is different from Earth's."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"The difference between a volcano and a corona--is it just the dried up lava that makes it a corona?"

"Geologic and atmospheric cycles are confusing."

"Planet classification, because it sounds like there are some exceptions."

"Trying to memorize everything about Venus that was being thrown at me was kind of challenging but it was made much easier when I previewed the presentation and read the bit on Venus."

"That Venus and Earth have outgassed similar amounts of carbon dioxide, only Earth's oceans have absorbed a large amount and is possible that Venus may have had oceans when it was young. Venus is now considered to be trapped in a runaway greenhouse effect."

Identify the relative amounts of these characteristics for Venus, compared to Earth. (Only correct responses shown.)

Volcanic outgassing, up until now: about the same as Earth [38%]
Heat from the sun: more than Earth [83%]
Amount of atmosphere, today: more than Earth [62%]
Interior core heat, today: about the same as Earth [35%]
Geologic activity, today: less than Earth [55%]

Identify the relative amounts of these characteristics for Mars, compared to Earth. (Only correct responses shown.)

Volcanic outgassing, up until now: less than Earth [72%]
Heat from the sun: less than Earth [82%]
Amount of atmosphere, today: less than Earth [90%]
Interior core heat, today: less than Earth [90%]
Geologic activity, today: less than Earth [69%]

Which jovian planet has the coolest interior temperatures?

Jupiter (most massive).	* [1]
Saturn (most prominent rings).	* [1]
Uranus (least active weather patterns).	******************** [20]
Neptune (farthest from the sun).	***** [5]
(Unsure/guessing/lost/help!)	** [2]

I believe Pluto should be a planet.

Strongly disagree.	** [2]
Disagree.	********** [10]
Neutral.	********** [10]
Agree.	**** [4]
Strongly Agree.	*** [3]

Briefly explain your answer to the previous question (whether Pluto should be a planet).

"Pluto is round and orbits the sun, but I don't think it dominates its orbit."

"Because the explanation given by the IAU made sense."

"Back in my day, we had nine planets."

"It doesn't change what the thing itself is, just what it's called. Simply fixing a mistake made many, many years ago."

"I don't truly know enough about it to decide."

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Do you think Pluto should be a planet? And why do you hate Pluto?" (It's not personal--simply, life is just not supposed to be fair.)

"When are we using the telescopes next?" (At the North County campus, we will project the image of the sun during October's partial solar eclipse, just after class that Thursday. And I'll also try to schedule another star night at the telescope shelter to look at the moon.)

Online reading assignment: applications of Newton's laws (friction)

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters on applications of Newton's laws (emphasizing static and kinetic friction).


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"A contact force perpendicular to the contact surface that prevents two objects from passing through one another is called a normal force. I also understand that a normal force only acts upon the contact surfaces and does not take other forces into account."

"Friction is caused by atomic or molecular bonds between the high points on the surfaces of two objects. We can never assume anything about the magnitude of the normal force."

"Kinetic friction is a force that seeks to stop motion. Static friction is a force to prevent movement from starting."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"The formulas! I still don't understand how to solve for these forces, or what all the different symbols mean."

"Separating Newtons three laws from each other. Knowing which law to apply to which situation."

"Some confusion over kinetic and static friction."

"While I understand these abstract concepts I am not confident in being able to apply all of them to problem solving. I look forward to going through problems in class to clear up misunderstandings I don't know I have and practice using this knowledge."

What is the meaning of the "normal" in the "normal force?"

"I have no idea."

"A weight or counter force to resist the weight."

"In geometry 'normal' means 'perpendicular.' Therefore normal force is always perpendicular to the contact surface."

The SI (Système International) units of the static friction coefficient µ_s and the kinetic friction coefficient µ_k are:

"Huh?"

"Newtons."

"They are dimensionless, as the units of the magnitudes of forces divided by each other cancel out."

"There are no units--the coefficients represent proportions (between the friction forces and normal force)."

Identify the magnitude of the static friction force f_s for each of the following situations of a box that is initially stationary on a horizontal floor. (Only correct responses shown.)

No horizontal forces applied to it, so it remains stuck to the floor:
f_s = 0. [60%]

A horizontal force applied to it, but still remains stuck to the floor:
f_s = some value between 0 and µ_s·N. [68%]

A horizontal force applied to it, at the threshold of nearly becoming unstuck:
f_s = µ_s·N. [54%]

Identify the magnitude of the kinetic friction force f_k for each of the following situations of a box that is already sliding across a horizontal floor. (Only correct responses shown.)

No horizontal forces on it, so it slows down:
f_k = µ_k·N. [19%]

A horizontal force applied in the forward direction, but not enough to keep the box going so it still gradually slows down:
f_k = µ_k·N. [17%]

A horizontal force applied in the forward direction, just enough to keep the box going at a constant speed:
f_k = µ_k·N. [41%]

A horizontal force applied in the forward direction, enough to gradually increase the speed of the box:
f_k = µ_k·N. [41%]

A horizontal force applied in the backwards direction, such that the box slows down:
f_k = µ_k·N. [21%]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"Where can we find the answers to all the quiz flashcard questions? I keep doing them but am not sure I am doing them right." (Come in to office hours or e-mail me your answers to flashcard questions not already discussed in class, so I can "grade" them and give you feedback on the ones you missed.)

"Can we talk about these homework questions in class, please? Can you do more explaining just in general?" (Yes, at the start of each class we'll go over the online reading assignments questions that the class messed up on most, before we move to working on example problems and flashcard questions. But I need the feedback on the reading assignments on what you specifically understand or don't understand in order to make the best use of time.)

"Since kinetic friction is basically proportional to the normal force and is independent of speed, and the object sliding and the surface the object is sliding on remain the same, isn't the kinetic friction force always f_k = µ_k·N?" (Yes--always! Good job.)

"In-class examples showing actual values being used for µ_s or µ_k would be good, just to have an idea of generally what these values look like." (Yes, as time allows, we'll go over some examples from previous quizzes and exams.)

"Once we obtain all numerical values for all the different types of forces, what equations do we use?" (The process of finding the numerical values for the forces is the point of using Newton's laws. Forcewise, there isn't much else to do afterwards, but if you have the acceleration from Newton's second law, then you can always calculate velocity and position from that using the kinematic equations.)

Physics quiz question: Space Shuttle "Launchbat"

Physics 205A Quiz 4, spring semester 2009
Cuesta College, San Luis Obispo, CA

Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Problem 6.22

"319336main_STS-119Bat4.jpg"
NASA
nasa.gov/mission_pages/shuttle/shuttlemissions/sts119/launchbat.html

An injured free-tailed bat (mass 0.012 kg[*]) latched onto the external fuel tank of the NASA Space Shuttle Discovery during liftoff[**] from sea level. Assume that g = 9.80 m/s² throughout this trajectory. If the bat held on until the external fuel tank separated from the Space Shuttle at an altitude of 110 km[***], the increase in gravitational potential energy of the bat was:
(A) 0.059 J.
(B) 6.5×10³ J.
(C) 1.3×10⁴ J.
(D) 1.4×10⁹ J.

[*] "12.3 g (0.43 oz)," wki.pe/Mexican_free-tailed_bat.
[**] "NASA—Bat Hung onto Shuttle During Liftoff," nasa.gov/mission_pages/shuttle/shuttlemissions/sts119/launchbat.html
[***] "59 nautical miles," spaceflight.nasa.gov/shuttle/reference/basics/index.html

Correct answer (highlight to unhide): (C)

The increase in gravitational potential energy of the bat is:

∆PE_grav = m·g·(y_f – y₀),

where the initial height y₀ = 0, such that:

∆PE_grav = (0.012 kg)·(9.80 N/kg)·(+110×10³ m – 0) = 12,936 J,

or to two significant figures, 1.3×10⁴ J.

(Response (A) is (1/2)·m·g; response (B) is (1/2)·m·g·y_f; while response (D) is m·g·(y_f)².)

Student responses
Sections 30880, 30881
(A) : 2 students
(B) : 2 students
(C) : 39 students
(D) : 0 students

Success level: 90%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.25

Astronomy current events question: Boraxino neutrino experiment

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Clara Moskowitz, "Strange Neutrinos from the Sun Detected for the First Time," August 27, 2014
http://www.scientificamerican.com/article/solar-neutrinos-detected-borexino/

Neutrinos produced by __________ were observed in a large underground water reservoir at Italy’s Gran Sasso National Laboratory.
(A) dark matter.
(B) the moon's gravitational forces.
(C) aurora borealis.
(D) fusion reactions in the sun.
(E) an ancient supernova explosion.

Correct answer: (D)

Student responses
Sections 70178, 70186
(A) : 3 students
(B) : 4 students
(C) : 5 students
(D) : 26 students
(E) : 2 students

Astronomy current events question: NASA ALICE instrument

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

D.C. Agle, Dwayne Brown, Maria Martine, Markus Bauer, "NASA Instrument aboard European Spacecraft Returns First Science Results," (no date given, web page accessed September 2014)
http://rosetta.jpl.nasa.gov/news/nasa-instrument-aboard-european-spacecraft-returns-first-science-results

The NASA "Alice" instrument aboard the European Space Agency’s Rosetta orbiter is collecting data on the __________ of comet 67P/Churyumov-Gerasimenko.
(A) erratic spinning.
(B) surface composition.
(C) tail.
(D) ice geysers.
(E) radioactivity.

Correct answer: (B)

Student responses
Sections 70178, 70186
(A) : 0 students
(B) : 23 students
(C) : 5 students
(D) : 7 students
(E) : 5 students

Astronomy current events question: reformatting Opportunity's memory

Astronomy 210L, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students are assigned to read online articles on current astronomy events, and take a short current events quiz during the first 10 minutes of lab. (This motivates students to show up promptly to lab, as the time cut-off for the quiz is strictly enforced!)

Guy Webster, "Memory Reformat Planned for Opportunity Mars Rover," (August 29, 2014; updated September 8, 2014)
http://www.jpl.nasa.gov/news/news.php?release=2014-292

In order to avoid future unplanned disruptions in its performance, NASA recently __________ of the Mars Exploration Rover Opportunity.
(A) reformatted the memory.
(B) cleaned off the solar panels.
(C) restarted the nuclear reactor.
(D) replaced the cracked wheel.
(E) dumped out its sample bin.

Correct answer: (A)

Student responses
Sections 70178, 70186
(A) : 34 students
(B) : 2 students
(C) : 2 students
(D) : 0 students
(E) : 1 student

Astronomy quiz question: October 2014 total lunar eclipse and partial solar eclipse

Astronomy 210 Quiz 2, fall semester 2014
Cuesta College, San Luis Obispo, CA

Observers in San Luis Obispo, CA will see a total lunar eclipse followed by a partial solar eclipse, both occurring in October 2014.[*][**] The total lunar eclipse would occur a few __________ before the partial solar eclipse.
(A) minutes.
(B) hours.
(C) days.
(D) weeks.

[*] eclipse.gsfc.nasa.gov/OH/OHfigures/OH2014-Fig03.pdf.
[*] eclipse.gsfc.nasa.gov/SEplot/SEplot2001/SE2014Oct23P.GIF.

Correct answer (highlight to unhide): (D)

The total lunar eclipse occurs when the moon is in its full phase (such that the moon will be in Earth's umbra); while for the partial solar eclipse the moon is in its new phase (such that observers on Earth are located in the moon's penumbra.) Since these two eclipses will occur within the same month, these must be consecutive full and new phases, which is approximately two weeks between these phases.

Section 70158
Exam code: quiz02n3w7
(A) : 8 students
(B) : 11 students
(C) : 6 students
(D) : 17 students

Success level: 41% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.62

Section 70160
Exam code: quiz02k3pL
(A) : 4 students
(B) : 2 students
(C) : 7 students
(D) : 21 students

Success level: 64% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.44

Astronomy quiz question: Saturn in retrograde

Astronomy 210 Quiz 2, fall semester 2014
Cuesta College, San Luis Obispo, CA

The diagram at right shows Saturn's position in the constellation Libra as seen by an observer in San Luis Obispo, CA. Saturn is currently undergoing retrograde motion. The following night Saturn will be __________ this position in the constellation Libra.
(A) slightly to the left of.
(B) slightly to the right of.
(C) exactly at.
(D) (Not visible at all the following night.)

Correct answer (highlight to unhide): (B)

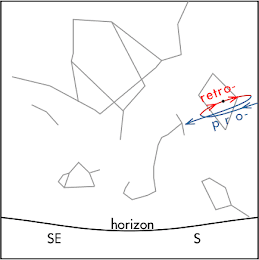When Saturn is undergoing prograde motion, it will move from west to east (in this perspective, right to left, as shown in blue) with respect to the background stars over consecutive nights. When Saturn is undergoing retrograde motion, it will move from east to west (in this perspective, left to right, as shown in red) with respect to the background stars over consecutive nights.

Section 70158
Exam code: quiz02n3w7
(A) : 15 students
(B) : 24 students
(C) : 3 students
(D) : 0 students

Success level: 59% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.74

Section 70160
Exam code: quiz02k3pL
(A) : 9 students
(B) : 20 students
(C) : 5 students
(D) : 0 students

Success level: 61% (including partial credit for multiple-choice)
Discrimination index (Aubrecht & Aubrecht, 1983): 0.56

Astronomy quiz archive: eclipses/history of astronomy

Astronomy 210 Quiz 2, fall semester 2014
Cuesta College, San Luis Obispo, CA

Section 71058, version 1
Exam code: quiz02n3w7


Section 71058

0- 8.0 :	** [low = 4.5]
8.5-16.0 :	******
16.5-24.0 :	************
24.5-32.0 :	********* [mean = 25.5 +/- 8.7]
32.5-40.0 :	************* [high = 40.0]

Section 71060, version 1
Exam code: quiz02k3pL


Section 71060

0- 8.0 :	** [low = 8.0]
8.5-16.0 :
16.5-24.0 :	***********
24.5-32.0 :	************ [mean = 26.5 +/- 7.8]
32.5-40.0 :	********* [high = 40.0]

Online reading assignment: atmosphere problems, Earth, the moon, Mercury (SLO campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on problems caused by the atmosphere for telescope observing, Earth, and the impacted worlds: the moon, and Mercury.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"I found it interesting that light from towns blocks us from seeing all the stars, I've noticed this when I go out camping but I never knew why I would see more stars out camping than in a city or anywhere with a lot of man-made light. Made me want to move."

"How the atmosphere can distort the views of space through our eyes and telescopes."

"That we have placed telescopes so high up (including mountain summits and space) in order to bypass atmospheric turbulence. It never occurred to me that seeing into space could be so obstructed by something like that."

"How volcanic activity emits carbon dioxide, and how our oceans not only help collect the water vapor from volcanic activity, but also absorbs carbon dioxide."

"I did not realize Mercury and the moon's appearance are so similar."

"I like the example of how carbon dioxide dissolved in the water because it is highly soluble in water--which explains the easy manufacture of carbonated beverages."

"I liked the turkey-cornish hen analogy. It made it easy to understand why bigger planets are hotter."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"Active optics versus adaptive optics. It makes it less distorted but smaller? How exactly does adaptive optics remove 'twinkling' movements in images of stars?"

"I'm wondering where the funding comes from for all of these satellites and spacecraft. This is personally confusing for me because I am so broke."

"I don't really understand why we use radio telescopes. I'm not sure what the benefit is of knowing that information."

Stars to appear to "twinkle" in the night sky because of:

"Distortions caused by telescopes."

"Much like looking up at the sky underwater the sky looks distorted from the motion of the water, making it appear differently. it is in the same sense that when looking at the sky at night the air distorts the sky making the stars look like they are twinkling."

"Atmospheric turbulence."

A large modern optical telescope in outer space would have images with better __________ than a comparable ground-based telescope.

brightness.	** [2]
resolution.	**************** [16]
magnification.	*** [3]
(None of the above choices.)	* [1]
(Two of the above choices.)	***** [5]
(All of the above choices.)	*********** [11]
(Unsure/guessing/lost/help!)	[0]

Identify how carbon dioxide enters and how it is taken out of Earth's atmosphere. (Only correct responses shown.)

Enters atmosphere from: volcanoes [61%]
Taken out of atmosphere by: oceans [53%]

Identify the oldest (longest ago) to the youngest (most recent) features on the moon. (Only correct responses shown.)

Craters partially filled in with flat lava plains: oldest (formed longest ago) [32%]
Flat lava plains: middle [55%]
Craters on top of flat lava plains: youngest (formed most recently) [45%]

Identify the oldest (longest ago) to the youngest (most recent) features on Mercury. (Only correct responses shown.)

Large crater basins: oldest (formed longest ago) [53%]
Lava-filled lowlands: middle [47%]
Long curving ridges: youngest (formed most recently) [68%]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"How do you differentiate between a star and a planet?" (To the naked eye, stars twinkle, but planets do not twinkle (and are also found in slightly different positions in the sky night after night).)

"If stars don't really twinkle, then why is there still movement shown in the adaptive optics *.GIF? (Removing twinkling using adaptive optics is not completely perfect, but only needs to be as good as the resolving power of the telescope. Any more correction is not going to matter.)

"What are the oldest parts of the moon and Mercury?" (We'll go over this in class, along with more details on adaptive optics.)

"I like this class. I've been studying a lot more for the second quiz since I did so poorly on the first one. I feel pretty confident in my comprehension of the material, but I did the first time too, so..." (Good luck, and try your best!)

Online reading assignment: Newton's third law

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on Newton's third law.


Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"When two objects interact they both exert a force on the other."

"I have a great understanding of Newton's first and second laws using the motion flow chart. It makes the questions much easier."

"Whereas Newton's first and second laws have to do with motion and net force, Newton's third law has to do with symmetry."

"Interaction pairs are formed when two objects are in contact with one another and exert equal, yet opposite, forces on each other. Not all equal/opposite forces are an interaction pair, as there must be two objects interacting with each other."

"Newton's third law says that interaction partners always have the same magnitude and are opposite in direction. Also, Newton's third law isn't involved every time two forces happen to be equal and opposite."

"One of the differences between Newton's first law and Newton's third law is that Newton's third law requires the same type of forces (weight-weight, etc.), whereas Newton's first law can involve two different types of forces."

"I understand the three-part checklist to determine if Newton's third law applies. If even one check fails, Newton's third law does not apply."

"One can describe the same force in two different ways because of Newton's third law."

"I understand that I need to do this reading!"

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I am confused by what it is talking about in 'a system.' I do not understand what it is distinguishing between an internal and external system."

"Newton's third law--specifically by in an interaction between two objects, whether/how each object's force is equal in magnitude to the other."

"I don't know how to distinguish between when Newton's first law applies and when Newton's third law applies. Also I wasn't 100% sure of the questions at the end of this form."

Consider two categories of motion: (1) Velocity that is constant and unchanging. (2) Velocity that is changing. Discuss whether or not there would be a third category of motion not already covered under these two categories.

"Something with no velocity?"

"How about velocity that is neither constant nor changing?"

"I am completely lost on this question and need to go over it in class."

"No, because either the acceleration is zero, or the acceleration is non-zero, which covers both categories."

"There would not be a third category--either velocity is constant or velocity is changing--it's a binary concept."

An "interaction pair" (or "interaction partners") refers to a pair of:

objects.	**** [4]
forces.	************************************ [36]
(Both of the above choices.)	***************** [17]
(Unsure/guessing/lost/help!)	[0]

According to Newton's first law, the normal force of the person's head on the stack of books is equal in magnitude and opposite in direction to the:

normal force of the stack of books on the person's head.	*************** [15]
weight force of Earth on the stack of books.	************************ [24]
(Both of the above choices.)	********* [9]
(Neither of the above choices.)	****** [6]
(Unsure/guessing/lost/help!)	*** [3]

According to Newton's third law, the normal force of the person's head on the stack of books is equal in magnitude and opposite in direction to the:

normal force of the stack of books on the person's head.	*************************** [27]
weight force of Earth on the stack of books.	**************** [16]
(Both of the above choices.)	****** [6]
(Neither of the above choices.)	**** [4]
(Unsure/guessing/lost/help!)	**** [4]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"If the net force is not zero then is the velocity not constant anymore? Do we use Newton's second law of motion? (Yes, and yes!)

"In any case involving two (interacting) objects, are there always at least two of Newton's laws in effect? For example, Newton's first law and third law, or Newton's second law and third law?" (Yes--either the first law or the second law in terms of the motion of the objects (constant or changing), and the third law in terms of how the objects interact with each other.)

"Are internal forces meant to be inside or something? Or is it more like forces within a set of objects, and we call them a 'system' because we want to look at the forces that they are contributing as a whole?" (Yes...and yes.)

"I am not sure how to differentiate between Newton's first law and Newton's third law for forces acting on/between the stack of books and the person's head. I also don't really understand the homework questions." (I'm going to allocate time to carefully go over these at the start of the next class.)

"It would be more helpful to have class discussions instead of working in groups and then going over the correct answers." (Sure, as long as you keep asking good questions for me to answer, either here on the reading assignments, or during class. That said, committing your answers in writing and then having a high-level discussion verifying how you got those answers with your peers is an important part of the learning process emphasized in this class.)

Physics quiz question: direction of motion on vx(t) graph

Physics 205A Quiz 2, fall semester 2014
Cuesta College, San Luis Obispo, CA

Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Problem 2.11

A v_x(t) graph of an object traveling along a straight line is shown at right. The object starts at x = 0 at t = 0. The object is traveling in the +x direction at:
(A) t = 1 s.
(B) t = 3 s.
(C) t = 5 s.
(D) (More than one of the above choices.)

Correct answer (highlight to unhide): (C)

From 0 s < t < 4.5 s, the object has negative v_x values, and thus is moving in the –x direction at t = 1 s and t = 3 s. From 4.5 s < t < 6 s, the object has positive v_x values, and thus is moving in the +x direction at t = 5 s.

Sections 70854, 70855, 73320
Exam code: quiz02T1o9
(A) : 3 students
(B) : 1 students
(C) : 35 students
(D) : 31 students

Success level: 50%
Discrimination index (Aubrecht & Aubrecht, 1983): 0.82

Online reading assignment: atmosphere problems, Earth, the moon, Mercury (NC campus)

Astronomy 210, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing presentations on problems caused by the atmosphere for telescope observing, Earth, and the impacted worlds: the moon, and Mercury.


Selected/edited responses are given below.

Describe something you found interesting from the assigned textbook reading or presentation preview, and explain why this was personally interesting for you.

"I did not know that most of our carbon dioxide came from volcanoes, so I thought that was pretty interesting."

"I didn't know that the ocean absorbed most of the carbon dioxide."

"Both interesting and confusing is that the moon was speculated to be formed originally from a fragment of a planet that collided with the Earth."

Describe something you found confusing from the assigned textbook reading or presentation preview, and explain why this was personally confusing for you.

"The amount of elements and processes that created Earth were somewhat unorganized in this textbook and without prior knowledge I would have been overwhelmed and confused."

"I wasn't confused."

"How to figure out the oldest and youngest features of Mercury or the moon, because you have to take into consideration a lot factors that could have caused each feature and what would happen as a result of this event or what would follow."

"That the moon was created by a fragment of a planet. How is that even possible that a fragment could form into a sphere?"

Stars to appear to "twinkle" in the night sky because of:

"Stars look like they are twinkling because we are viewing them through the turbulence of the atmosphere."

"The air of our atmosphere is turbulent. There is constant disturbance in the traveling light due to that, especially if the light has to travel through a lot of the atmosphere, as it does if the stars are only a few degrees from the horizon."

A large modern optical telescope in outer space would have images with better __________ than a comparable ground-based telescope.

brightness.	*** [3]
resolution.	****** [6]
magnification.	** [2]
(None of the above choices.)	* [1]
(Two of the above choices.)	****** [6]
(All of the above choices.)	******* [7]
(Unsure/guessing/lost/help!)	** [2]

Identify how carbon dioxide enters and how it is taken out of Earth's atmosphere. (Only correct responses shown.)

Enters atmosphere from: volcanoes [67%]
Taken out of atmosphere by: oceans [59%]

Identify the oldest (longest ago) to the youngest (most recent) features on the moon. (Only correct responses shown.)

Craters partially filled in with flat lava plains: oldest (formed longest ago) [48%]
Flat lava plains: middle [44%]
Craters on top of flat lava plains: youngest (formed most recently) [67%]

Identify the oldest (longest ago) to the youngest (most recent) features on Mercury. (Only correct responses shown.)

Large crater basins: oldest (formed longest ago) [59%]
Lava-filled lowlands: middle [41%]
Long curving ridges: youngest (formed most recently) [56%]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"We're getting a new space telescope in 2018? Dude, yes I am so pumped for better pictures of the universe. Current images of nebulae and galaxies are rad as all get out, but will this telescope be better. Very cool."

"What is your favorite pastime? How did you meet Mrs. P-dog?" (Swing dancing, especially when I get to DJ at the Madonna Inn on Monday nights. Which is how I first met Mrs. P-dog.)

Online reading assignment: forces and motion

Physics 205A, fall semester 2014
Cuesta College, San Luis Obispo, CA

Students have a weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.

The following questions were asked on reading textbook chapters and previewing a presentation on forces and motion.

Selected/edited responses are given below.

Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.

"I understand that Newton's first law applies when the net force acting on an object is zero, and the object has a constant speed and a constant direction. I also understand that Newton's second law of motion states that an object's acceleration is proportional to the net force acting on it and inversely proportional to its mass."

"Newton has three laws, but only two of them classify motion. The first law applies to an object that has a constant speed and constant direction or when a net force that equals zero. The second law applies to an object that does not have constant speed or constant direction or when a net force does not equal zero."

"Newton's first law works with objects traveling at a constant speed, in a constant direction. Or it does not move at all. Then the second law states that an object will not move unless it has some force to make it move."

"The difference between Newton's first and second law. I also know when to use which law."

"Newton's first law, how no force is required to keep an object in motion if there are no forces opposing its motion."

"The motion flowchart, in that if an object's speed and direction are constant we can apply Newton's first law. If either of the two aren't constant, we use Newton's second law."

"A change in movement for an object only happens if a force is applied. This includes gravity or air resistance. Inertia refers to an object's tendency to resist movement. The amount of mass and the inertia of it are closely related. The smaller the mass the less inertia it will have."

Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.

"I found Newton's laws to be a bit confusing and how to apply them to situations. Like the zero and non-zero net forces."

"The relationship that constant speed and constant direction have with the first and second law. Having trouble getting the differences between the laws."

Identify whether a zero or non-zero net force corresponds to Newton's first law or Newton's second law. (Only correct responses shown.)

Zero net force (ΣF = 0): Newton's first law ("N1") [88%]
Non-zero net force (ΣF ≠ 0): Newton's second law ("N2") [86%]

For the rocket sled, Newton's __________ law applies to the motion of this object, and the forces acting on the object add up to a __________ net force.

first; zero.	************* [13]
second; non-zero.	****************************************** [42]
(Unsure/guessing/lost/help!)	** [2]

While the F-35B is descending (before it touches the ground), Newton's __________ law applies to the motion of this object, and the forces acting on the object add up to a __________ net force.

first; zero.	****************************** [30]
second; non-zero.	***************** [17]
(Unsure/guessing/lost/help!)	********** [10]

For this car with a steady speedometer reading (and assuming the shaking is due to the person holding camera, and not from moving the car itself), Newton's __________ law applies to the motion of this object, and the forces acting on the object add up to a __________ net force.

first; zero.	****************************************** [42]
second; non-zero.	********** [10]
(Unsure/guessing/lost/help!)	***** [5]

For a person in the swinging chair ride moving along a circular trajectory at a constant speed, Newton's __________ law applies to the motion of this object, and the forces acting on the object add up to a __________ net force.

first; zero.	************************** [26]
second; non-zero.	*************************** [27]
(Unsure/guessing/lost/help!)	**** [4]

For this car with a zero speedometer reading, Newton's __________ law applies to the motion of this object, and the forces acting on the object add up to a __________ net force.

first; zero.	****************************************** [42]
second; non-zero.	********** [10]
(Unsure/guessing/lost/help!)	***** [5]

Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.

"These motion examples are confusing because I don't fully understand how to apply Newton's Laws to them. We should quickly discuss these examples in the next class if there is time." (Yes. We totally should.)

"What questions can one ask oneself to determine whether it is Newton's first law or second law? (What questions? These questions. And these other questions.)

"Are the first two laws different in that one has no acceleration and the other doesn't, or is there more to it?" (Awesome--that's exactly how Newton's first two laws work.)