Physics presentation: ideal fluid flow

When this pump or vacuum system is started, air begins to flow through this hose, which has a slight crimp, and as a result this hose begins to totally collapse. Now don't you say it's because of suction, because as you know, physics don't suck. (It blows.) (Video link: "hose collapse.")

In a previous presentation we investigated the behavior of static fluids, now we'll consider dynamic fluids--more specifically, ideal fluid flow. First we'll define what we mean by "ideal" fluids, then we'll see how two conservation laws are applied simultaneously to flowing ideal fluids.

Ideal fluids fall under a restrictive class of fluids--let's take a look at the characteristics that set ideal fluids apart from, say, real fluids.

Ideal fluids are incompressible, which water is to some extent. Note that while air is not incompressible, there are situations where we can make the crude approximation that it is.

An ideal fluid should undergo laminar flow, where the adjacent particles flow smoothly past each other, as opposed to turbulent flow, where particles swirl around in a chaotic manner. Like many fluids water can undergo both laminar and turbulent flow, so we'll restrict our attention to certain conditions where water undergoes laminar flow.

Lastly, an ideal fluid should be non-viscous, that is, flow without appreciable frictional losses, as opposed to a viscous fluid that, well, looks and is literally, "gooey." (Video link: "Viscosity.")

Streamlines are a way to visualize ideal fluid flow. Here air is undergoing incompressible, laminar, non-viscous flow over the front end of a car in this wind tunnel, where the streamlines are smoothly conforming to the contours of the car and to adjacent streamlines. Note the rear of the car, where the streamlines are turbulent, and indicate the presence of non-ideal fluid flow. (Video link: "Mercedes-Benz SLS AMG Developement and Testing Wind tunnel.")

The first conservation law for ideal fluid flow follows from its incompressible nature.

Even if a pipe changes radius, the incompressibility of an ideal fluid means that the same volume flowing in one end must equal to the same volume coming out the other end in the same amount of time. "Stuff in, stuff out."

This conservation of volume flow rate can be reinterpreted in terms of cross-sectional areas and fluid speeds in the continuity equation. A large-area section of pipe will have a slower fluid speed than a small-area section of the same pipe, which will have a faster fluid speed. Note that the product of cross-sectional area and fluid speed at any section of a pipe results in the volume flow rate.

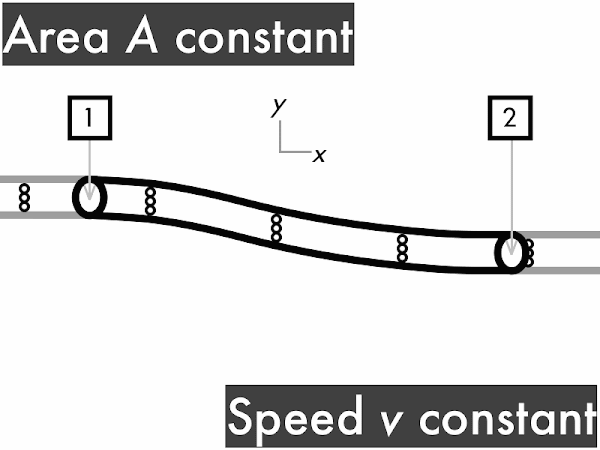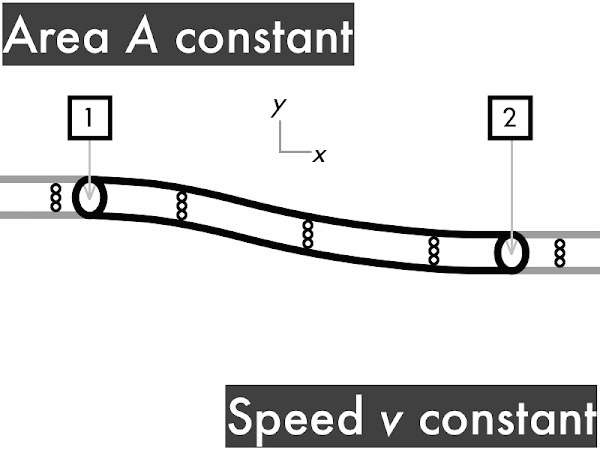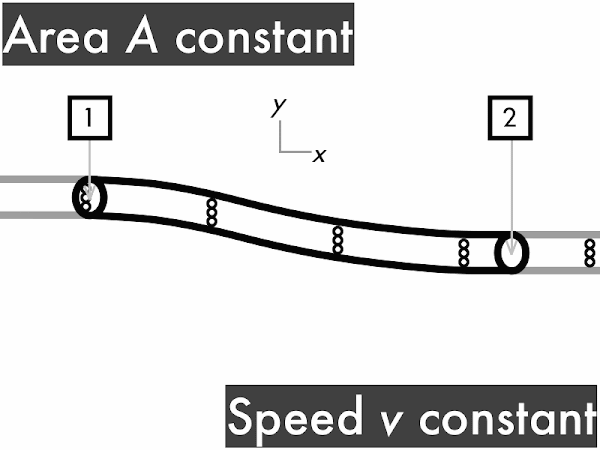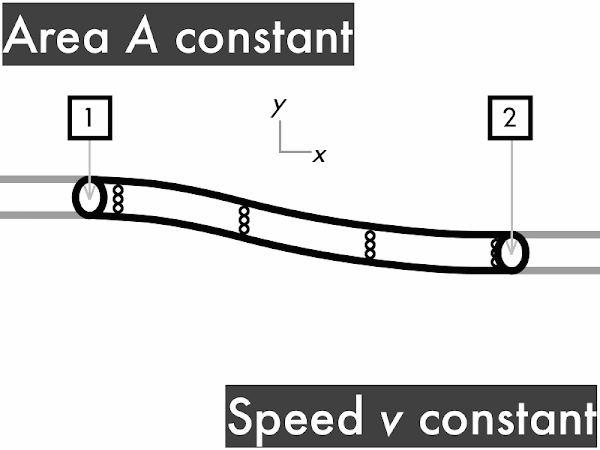
For a pipe with a constant cross-sectional area, the volume flow rate ∆V/∆t through the pipe is constant. To convince yourself of this you'll need a friend to watch this animation with you. Every time you see fluid particles entering the pipe, say "in." "In. In. In..." Keep doing that. Convince your friend to say "out" every time fluid particles are leaving the pipe. "Out. Out. Out..." If the two of you do this correctly, each time you say "in," your friend immediately follows-up by saying "out." This means that rate of fluid volume going in (represented here by three dots) must continuously be equal to the rate of fluid volume going out. "Stuff in, stuff out," right?

Then from the continuity equation:

A₁·v₁ = A₂·v₂,

since the cross-sectional areas of where the fluid goes in and where it goes out are the same (A₁ = A₂), then v₁ = v₂, so the speed of the fluid flowing through this pipe must be constant as well.

For a pipe with increasing cross-sectional area, the volume flow rate ∆V/∆t through the pipe is also constant. Let's do the same "in and out" exercise as above. Every time you see fluid particles entering the narrow end of the pipe, say "in," while your friend says "out" every time fluid particles are leaving the wider end of the pipe. "In. Out. In. Out. In. Out..." As before, since each time you say "in," your friend immediately follows-up by saying "out," so the rate of fluid volume going in the narrow end (represented here by three dots) must continuously be equal to the rate of fluid volume going out the wider end. "Stuff in, stuff out," right?

Then from the continuity equation:

A₁·v₁ = A₂·v₂,

since the cross-sectional area of where the fluid goes in is smaller than the cross-sectional area of where it goes out (A₁ < A₂), then v₁ > v₂, so the speed of the fluid flowing through this pipe slows down.

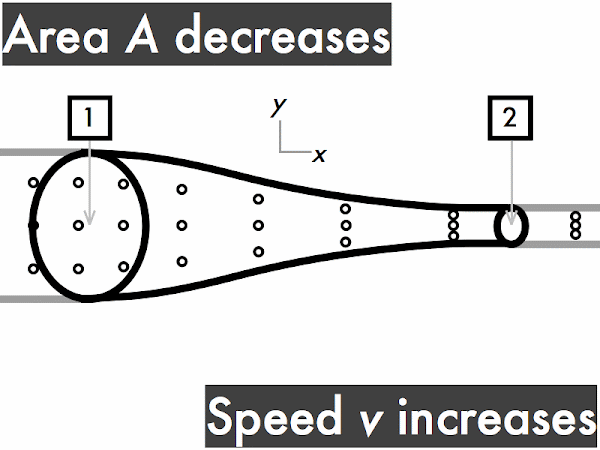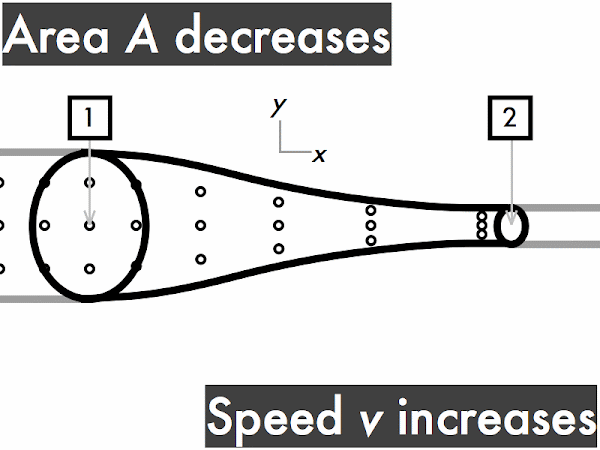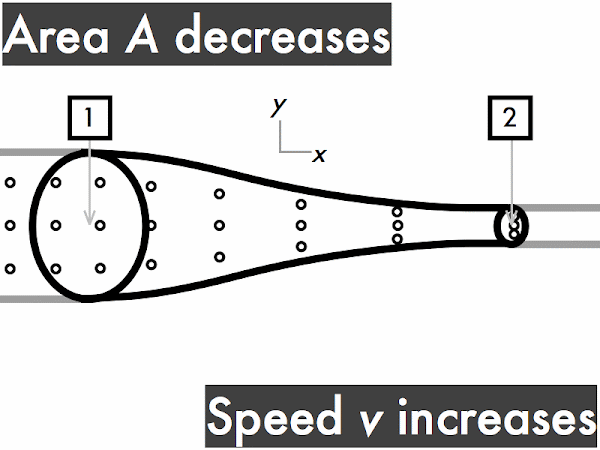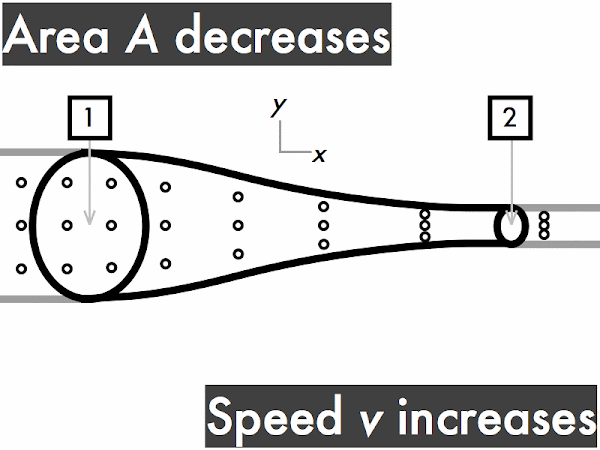
Conversely, for a pipe with decreasing cross-sectional area, the speed of the fluid through this pipe must have a corresponding increase, such that it flows more quickly through the narrow portion of the tube.

The second conservation law for ideal fluid flow follows from its laminar, non-viscous nature, as energy per volume density will be conserved if there are no losses to dissipative turbulence and frictional losses. (Incompressibility matters here too, such that the volume term in the energy per volume will be conserved.)

Bernoulli's equation is the extension of the static fluid relationship between pressure and gravitational potential energy per volume changes, to ideal fluid flow, with the addition of a translational kinetic energy per volume term. All three terms have equivalent units of Pa or J/m³, such that they can transfer to/from each other, as long as the net balance of exchanges is zero.

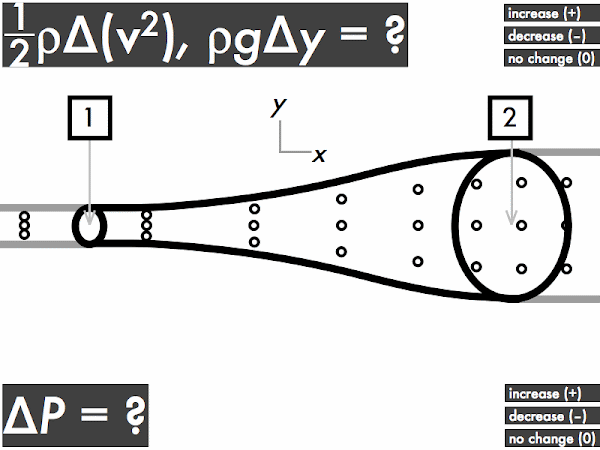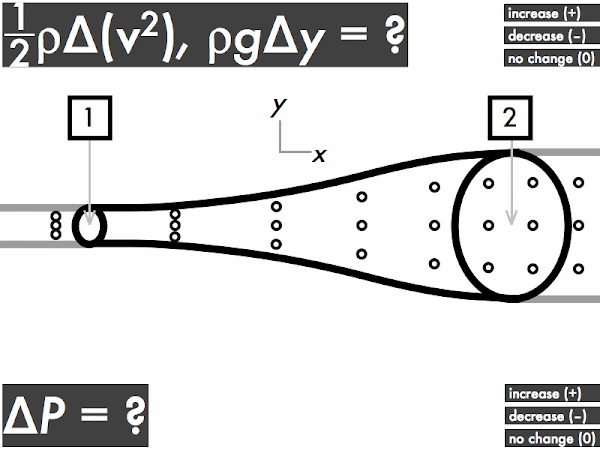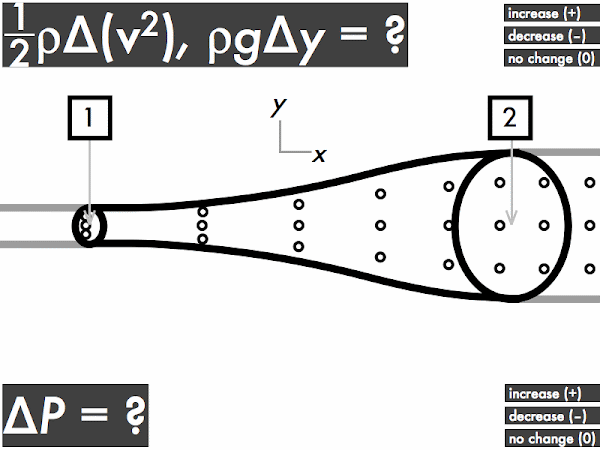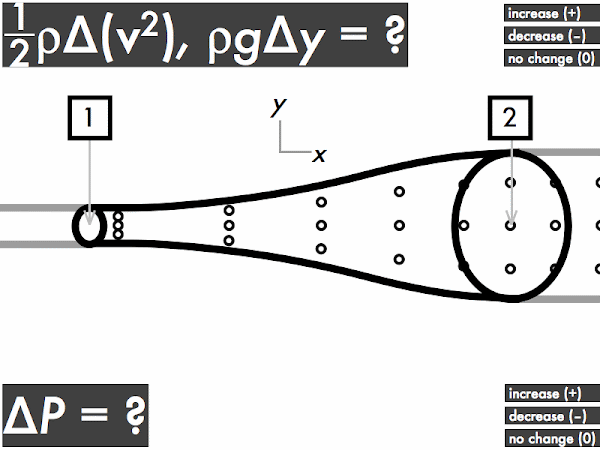
For an ideal fluid flowing through a horizontal pipe with a widening cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? Let's refer back to the continuity equation discussion above and recall that while the volume flow rate doesn't change, the speed changes, where the fluid slows down travels through this pipe. This means that the kinetic energy density will decrease (as it depends on the square of the speed), and this term will be negative.

Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change? Since the center of the pipe has no change in height (even though the cross-sectional areas are different, they are still "horizontally aligned" with each other), there is no change in the gravitational potential energy density term, and this term will be zero.

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change? Note the steps in determining the changes (if any) in pressure for this ideal flowing fluid--first we apply the continuity equation to determine the change in speeds (if any), which tells us the change (if any) in the kinetic energy density. We then look at the change in height of the centerline of the pipe (if any), which tells us the change (if any) in the gravitational potential energy density. Then we can look at Bernoulli's equation:

0 = ∆P + ρ·g·∆y + (1/2)·ρ·∆(v²),

and look at the increases (+) or decreases (–) (or no changes) of the terms we know so far:

0 = ∆P + (0) + (–).

In order to balance out this equation to equal zero on the left-hand side, the pressure of the fluid as it flows through this pipe must increase, making ∆P positive, such that:

0 = (+) + (0) + (–),

and both sides of Bernoulli's equation are balanced. So for this ideal fluid flowing through this widening pipe, the pressure will increase. This is why a weakened, enlarged blood vessel (an aneurysm) is dangerous, as blood flowing through this damaged, wider section will temporarily experience an increase in pressure as it slows down, and may widen the blood vessel even more and cause it to eventually rupture.

For an ideal fluid flowing through a horizontal pipe with a narrowing cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? (Refer back to the continuity equation discussion to determine this.) Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change?

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change?

(Note that the pressure should decrease in the narrow portion of this pipe, which is why the crimped hose at the start of this presentation collapsed--as air flowed through the narrow crimped portion of the hose, its speed increased, which made the pressure decrease inside the hose, and the surrounding atmospheric pressure then flattened the crimped portion even further.)

For an ideal fluid flowing through a descending horizontal pipe with a constant cross-sectional area, does the kinetic energy density term (1/2)·ρ·∆(v²) term increase, decrease, or have no change? (Refer back to the continuity equation discussion to determine this.) Does the gravitational potential energy density term ρ·g·∆y term increase, decrease, or have no change?

Then as a result, does the pressure of the ideal fluid flowing through this pipe increase, decrease, or have no change?