Physics presentation: torque and rotations

Whatever that "Nutcracker" gadget is, looks like this mechanic is going to need one to remove that stuck lug nut. We'll consider why he is probably not going to succeed, just doing what he's doing here. (Video link: "The Nutcracker - Undo Truck Wheel Nuts Easily.")

Also we'll analyze why this crane boom came crashing down in this industrial accident. (Video link: "Crane Accident - Australia....")

Here we will introduce torques and static equilibrium, much like how we developed ideas of forces and translational equilibrium, but applied here to rotations.

First, let's define torque, and some examples of how to calculate torque.

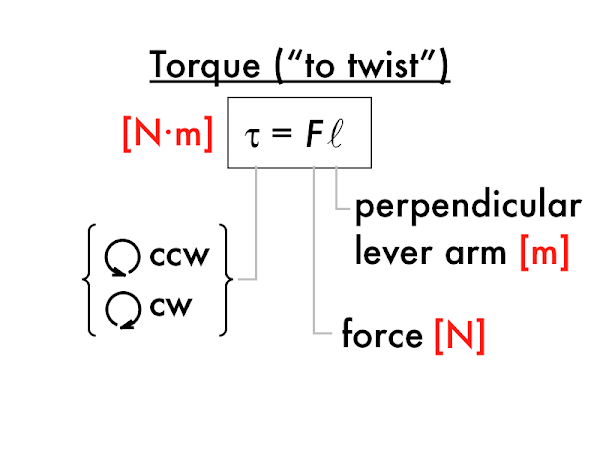
We'll emphasize a certain method of finding the torque ("the twisting") that a force exerts on an object, by using a perpendicular lever arm ℓ (sometimes called the "moment arm"). The resulting product of the force and lever arm results in the torque, in units of N·m (which in this context should not be thought of as joules), and can either have a counterclockwise or clockwise direction.

Let's revisit our hapless mechanic, who is trying two different ways to exert as much torque as possible on a lug nut. Consider the force exerted by the mechanic on the wrench (or spanner, since this shop is in Australia) be his entire weight, downwards. We've identified the lug nut, our pivot point, with a dot.

Extend a line along this force vector--this is the line of action, which is just a guide to find the perpendicular lever arm, which starts at the pivot point, and at the other end must intersect the line of action perpendicularly. In this case (but not always) the perpendicular lever arm corresponds to the physical object. The magnitude of the torque is the product of the lever arm distance (in m), and the magnitude of the force (in N). Since this force would rotate the object counterclockwise, then this is a counterclockwise torque.

Now for the second case, again extend the line of action along the force vector, and draw in the perpendicular lever arm, which starts at the pivot point, and must intersect the line of action perpendicularly. Note that in this case (as does sometimes happen) the perpendicular lever arm does not correspond to a physical object. Since this force would also rotate the object counterclockwise, this would also be a counterclockwise torque.

Compare both cases side-by-side--because the force magnitudes (the weight of the mechanic) and the perpendicular lever arm distances are approximately the same, then the torque exerted in either case is approximately the same! (How should the mechanic use the spanner to exert a greater amount of torque on the nut?)

Second, let's apply Newton's first law and second law to rotational motion.

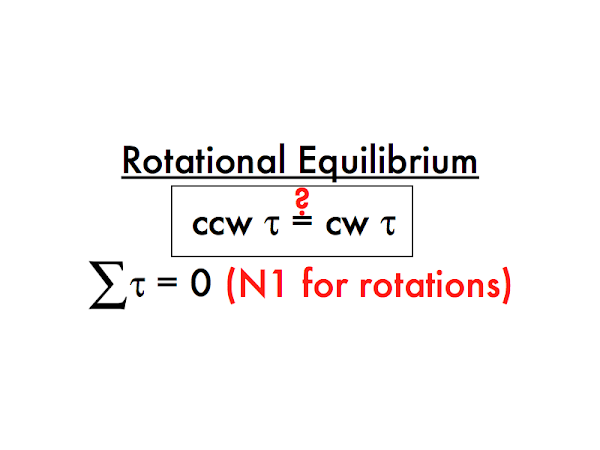
Recall Newton's first law for vertical motion, where all of the up forces on an object would be balanced by all of the down forces on an object, such that the object's vertical motion would either be stationary, or have a constant vertical motion. (Similarly for Newton's first law for forces and motion along the horizontal direction.)

Similarly there is also a Newton's first law for rotational motion, where all of the counterclockwise torques on an object would be balanced by all of the clockwise torques on an object, such that the object would either be stationary, or have a constant rotational motion. This is the equivalent statement of saying that all the torques acting on that object add up to zero.

If you are looking forward to a career in structural engineering, then welcome to the rest of your life--keeping buildings and other structures from collapsing is all about getting the torques (and forces) to balance out (or sum to zero). Good times.

Returning to the falling crane example, let's take a look at each of the two forces that exert torques on the crane. The black-and-white checkered circle represents the center of gravity, the single point on the object at which the weight force can be considered to be acting. Then extending the line of action for the weight force allows its perpendicular lever arm to be identified, which in this case does not coincide with the physical crane. The magnitude of the weight torque is the product of the perpendicular lever arm (in m), and the magnitude of the weight (in N). Since the weight force would rotate the object clockwise, then this torque is clockwise.

Next, the cable at the end of the crane as the other force exerting a torque on it. Extending the line of action for the tension force at the end of the crane allows its perpendicular lever arm to be identified, which also in this case does not coincide with the physical crane. The magnitude of the tension torque is the product of the perpendicular lever arm (in m), and the magnitude of the tension force (in N). Since the tension force would rotate the crane counterclockwise, then this torque would be counterclockwise.

If the counterclockwise torque from the tension force balanced out the clockwise torque from the weight force, then the crane would remain stationary. However, since the crane starts to rotate clockwise, these torques do not balance, as the clockwise torque from the weight force is greater than the torque from the tension force. There really should have been more tension force pulling up on the end of the crane. Oh well...

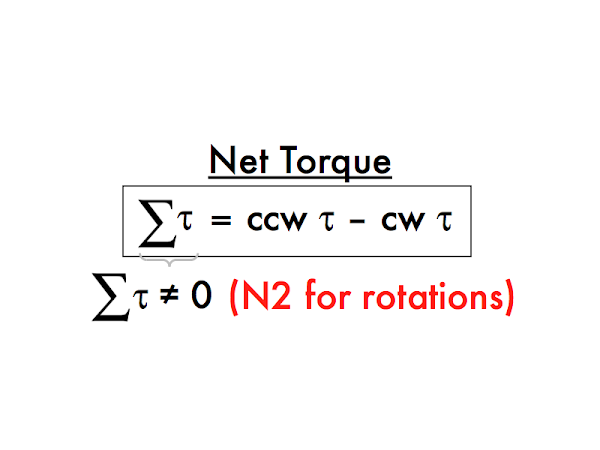
What would Newton's second law for rotations look like? If all the counterclockwise torques and clockwise torques on an object don't balance out, then the net torque can be calculated by adding the counterclockwise torques (which are positive) with the clockwise torques (which are negative, because those correspond to rotations in the opposite direction). Right now, the emphasis is on recognizing whether Newton's first law for rotations (zero net torque) or Newton's second law (non-zero net torque) for rotations apply to an object.

Because sometimes a non-zero net torque is needed, in order to make a object begin to rotate...

Or sometimes you want a zero net torque on an object, to keep it from rotating--whoops!