Cuesta College, San Luis Obispo, CA
Students have a bi-weekly online reading assignment (hosted by SurveyMonkey.com), where they answer questions based on reading their textbook, material covered in previous lectures, opinion questions, and/or asking (anonymous) questions or making (anonymous) comments. Full credit is given for completing the online reading assignment before next week's lecture, regardless if whether their answers are correct/incorrect. Selected results/questions/comments are addressed by the instructor at the start of the following lecture.
The following questions were asked on reading textbook chapters and previewing a presentation on ideal fluid flow.

Selected/edited responses are given below.
Describe what you understand from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically demonstrate your level of understanding.
"Fluid flow can be steady or unsteady. Velocity at any point is constant as time passes for a steady flow. Unsteady flow exists whenever the velocity at a point in the fluid changes as time passes. Fluids can also be compressible or incompressible, most being nearly incompressible. Fluid flow can be viscous or nonviscous. A viscous fluid does not flow readily but a non-viscous one, like water, does."
"Ideal fluid flow has the following characteristics; incompressible, laminar, and non-viscous. I understand how volume flow rate conservation law that comes from its incompressible nature uses the continuity equation. And how the energy density conservation law uses Bernoulli's equation."
"Fluid flow can be steady or unsteady; Unsteady flow exists whenever the velocity at a point in the fluid changed as time passes, Turbulent flow is an extreme kind of unsteady flow and occurs when there are sharp obstacles or bends in the path of a fast moving fluid. Fluid can be compressible or incompressible, fluid flow can be viscous or non-viscous."
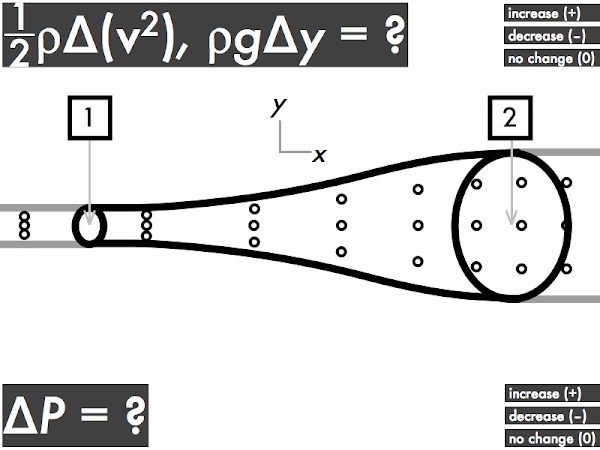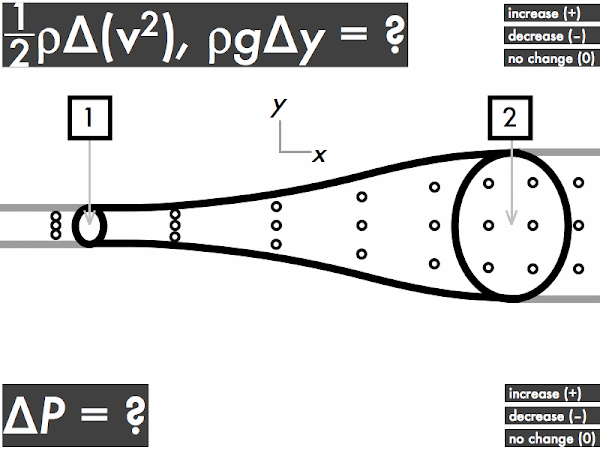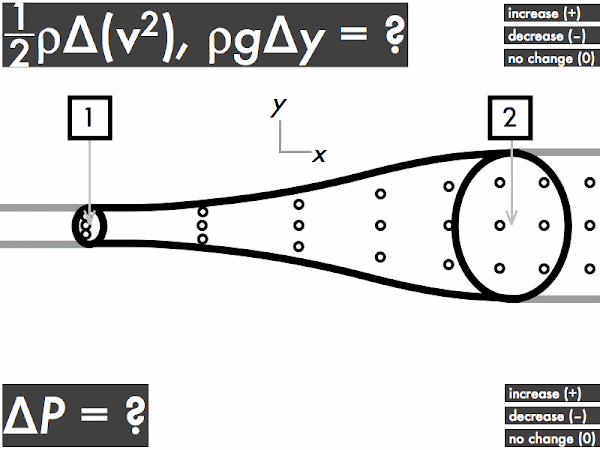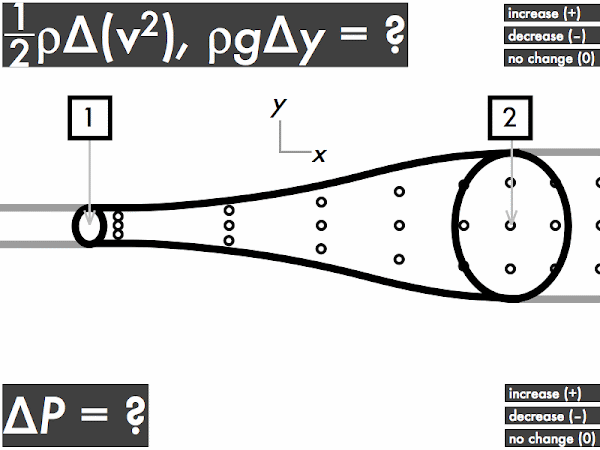
"I understand that when an ideal fluid flows through a pipe with a widening cross sectional area, the velocity of the fluid will slow down, kinetic energy decreases and the pressure will increase. When an ideal fluid flows through a pipe with a narrowing cross sectional area, the velocity of the fluid will increase, kinetic energy is increases and the pressure will decrease."
"As the area decreases the fluid speed increases. when elevation decreases the fluid speed also increases. Bernoulli's equation relates the density, pressure, fluid speed and elevation at two separate points."
Describe what you found confusing from the assigned textbook reading or presentation preview. Your description (2-3 sentences) should specifically identify the concept(s) that you do not understand.
"I seemed to understand this subject, but completely differentiating between the properties of ideal fluid flow will need more practice. What seemed somewhat confusing or a little more review in class are volume flow conservation and energy density conservation, and exactly how to apply the continuity equation to volume flow rate conservation law and the Bernoulli's equation to energy density conservation law."
"Bernoulli's equation definitely seems ominous. I can see the relation between energy conservation and this topic. However, hopefully after the homework problems I'll be more comfortable with it."
"I am confused about when to use Bernoulli's equation and how the concepts of the work-energy theorem relates to this equation. I am confused by what is meant by how elevation changes the various variables as well."
"I don't understand when the pressure or density changes, or how to know when y changes, how that works with/ against the change in area. I dont understand how to calculate anything, lost :("
"I didn't quite understand Bernoulli’s equation. The equations itself looked very complicated and when the book didn’t really provide an example problem and I feel like I just learn better that way so maybe that’s why I feel like I didn’t understand how to use the equation."
"This chapter seemed to hold a mess of equations that I don't know when to use or how to use them; however, it seems similar to the set-up of our previous conservation equations in which we ignore one side of the equation and can determine whether each piece on the right side of the equation is increasing or decreasing."
"How Bernoulli's equation relates to the work-energy theorem."
"I don't understand anything yet."
What is the SI (Système International) unit for volume flow rate?
"m3/s."
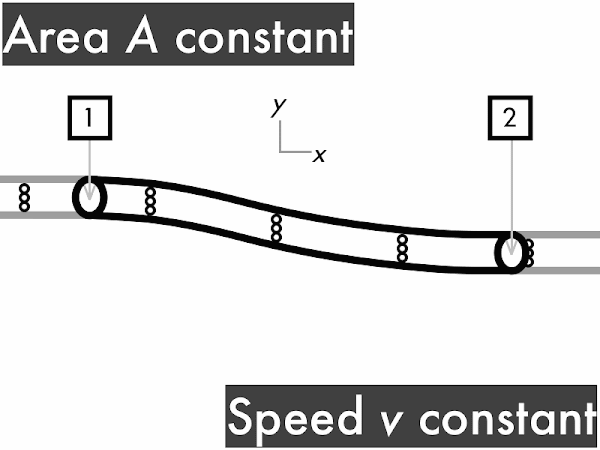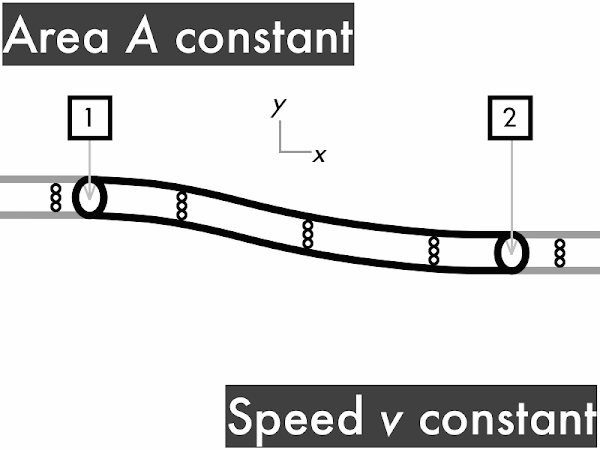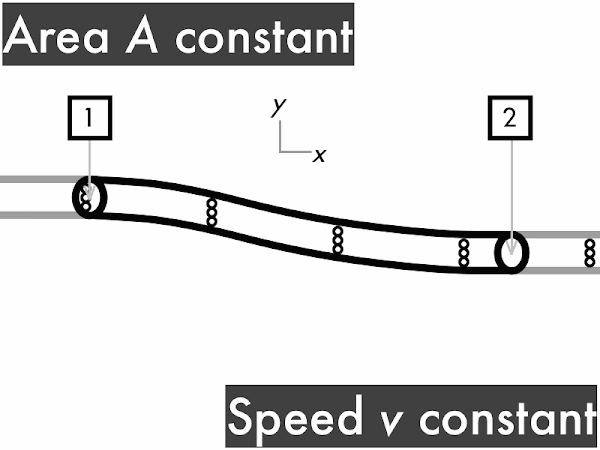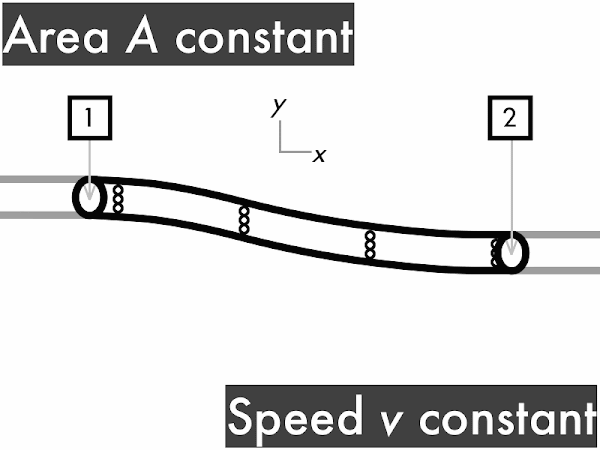
decreases. [0] remains constant. **************************************** [40] increases. **** [4] (Unsure/lost/guessing/help!) ** [2]

decreases. ************************* [25] remains constant. ********* [9] increases. ********** [10] (Unsure/lost/guessing/help!) ** [2]
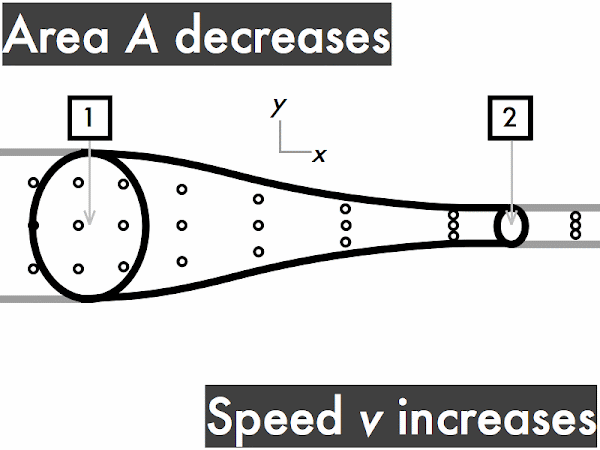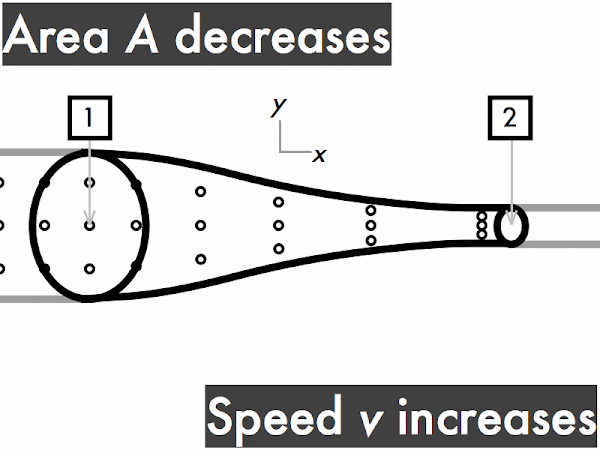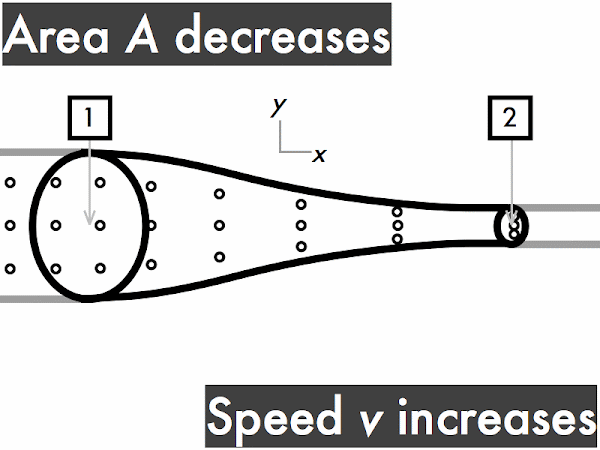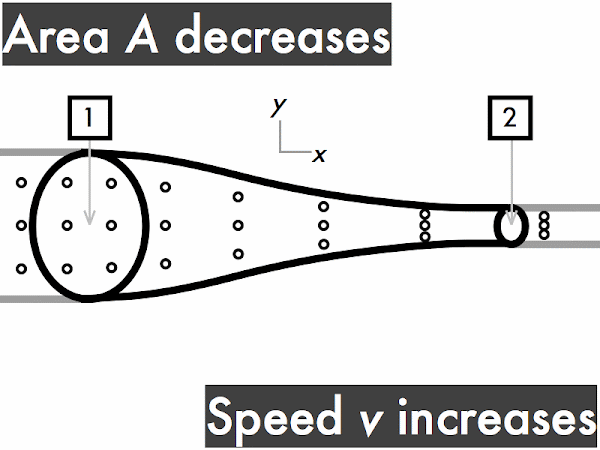
decreases. ********** [10] remains constant. ******* [7] increases. *************************** [27] (Unsure/lost/guessing/help!) ******* [2]
(Only correct responses shown.)
(1/2)·ρ·∆(v2): decreases [54%]
ρ·g·∆y: no change [52%]
∆P: increases [33%]

(Only correct responses shown.)
(1/2)·ρ·∆(v2): increases [57%]
ρ·g·∆y: no change [54%]
∆P: decreases [37%]

(Only correct responses shown.)
(1/2)·ρ·∆(v2): no change [89%]
ρ·g·∆y: decreases [33%]
∆P: increases [74%]
Ask the instructor an anonymous question, or make a comment. Selected questions/comments may be discussed in class.
"If cross-sectional area is changing, do we assuming that particles are still moving in a straight line with no vertical deviation?" (Yes, if flow is laminar all the streamlines will be parallel to each other, either scrunching together or spacing apart without crossing. #whateveryoudodontcrossthestreams.)
"Great presentation GIFs. Super-helpful for understanding the material."
"Your drawings make everything better. shout out to visual learners."
"Go over these as you normally do, thank you!"
"Now you know why I don't want to be a physics major. I want to just live my life with plants and dirt."
No comments:
Post a Comment