Cuesta College, San Luis Obispo, CA
Cf. Giambattista/Richardson/Richardson, Physics, 2/e, Problem 23.11, Comprehensive Problem 23.91
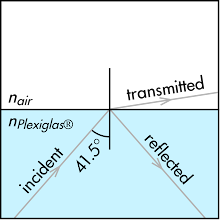Light in Plexiglas® (index of refraction[*] of 1.491) is incident at an angle of 41.5° at the interface between Plexiglas® and air (index of refraction of 1.000). (Drawing is not to scale.) If the incident angle of the beam of light in Plexiglas® is increased slightly from 41.5° to 42.0°, describe what will happen to the beam. Explain your reasoning using the properties of light and refraction. [*] wiki.pe/Acrylic_glass.
Solution and grading rubric:
- p:
Correct. With an incident angle less than the critical angle, light will still be transmitted out into air instead of totally internally reflected back into Plexiglas® (there will also be a partially reflected ray in Plexiglas® as well). Directly calculates the critical angle to compare to the incident angle, or attempts a (successful) trial solution for the transmitted angle in air using Snell's law. - r:
As (p), but argument indirectly, weakly, or only by definition supports the statement to be proven, or has minor inconsistencies or loopholes. - t:
Nearly correct, but argument has conceptual errors, or is incomplete. - v:
Limited relevant discussion of supporting evidence of at least some merit, but in an inconsistent or unclear manner. - x:
Implementation/application of ideas, but credit given for effort rather than merit. - y:
Irrelevant discussion/effectively blank. - z:
Blank.
Sections 30882
Exam code: finalpL3x
p: 19 students
r: 1 student
t: 5 students
v: 5 students
x: 0 students
y: 0 students
z: 0 students
A sample "p" response (from student 1408), first attempting a trial solution to Snell's law (which would indicate no total internal reflection):
Another sample "p" response (from student 6377), explicitly solving for the critical angle first, and then noting that the incident angle is smaller than the critical angle:
No comments:
Post a Comment